Disequazioni in due variabili: come si calcolano
Calcolare le disequazioni in due variabili è un argomento fondamentale in matematica, essenziale per comprendere e risolvere problemi che coinvolgono relazioni tra due quantità variabili. Una disequazione in due variabili è simile a un’equazione, ma invece di indicare l’uguaglianza tra due espressioni, mostra una relazione di disuguaglianza, come “minore di", “maggiore di", “minore o uguale a", o “maggiore o uguale a".
Il processo di calcolo di una disequazione in due variabili inizia con la definizione della disequazione stessa. Si può considerare, ad esempio, una forma lineare come “ax + by > c", dove “x" e “y" sono le variabili e “a", “b" e “c" sono costanti. Il passo successivo è determinare la regione del piano cartesiano che soddisfa questa disuguaglianza. Questo solitamente comporta l’identificare la regione al di sopra o al di sotto della linea rappresentata dall’equazione corrispondente (quando la disequazione è cambiata in un’equazione).
Un aspetto fondamentale nel calcolo delle disequazioni in due variabili è la rappresentazione grafica. Il grafico fornisce una visualizzazione immediata della regione di soluzione, permettendo di vedere quale parte del piano soddisfa la disequazione. Spesso, questo coinvolge l’ombreggiare l’area appropriata sul piano cartesiano.
Vediamo come fare passo per passo.
Disequazioni in due variabili: come si risolvono
Disequazioni lineari
Disequazioni non lineari
Come risolvere le disequazioni che hanno due variabili? Le disequazioni in una variabile danno come soluzione un intervallo oppure una unione di intervalli. In generale siamo in una dimensione. Quindi una variabile = una dimensione. Se le variabili sono due allora la soluzione sarà in due dimensioni. Ma cosa vuol dire? E’ facile.
Partiamo da £$y=x$£. Le soluzioni di questa equazione sono tutti i punti della retta bisettrice del I e III quadrante. Quali saranno le soluzioni di £$y>x$£? Sono tutti i punti che hanno l’ordinata maggiore dell’ascissa, cioè tutti i punti che sono “sopra" la retta £$y=x$£.
L’insieme di questi punti rappresenta un semipiano, che ha quindi due dimensioni. Le disequazioni in due variabili si risolvono graficamente sul piano cartesiano:
1. metti £$=$£ al posto del segno di disuguaglianza;
2. disegna la curva;
3. la soluzione è la parte di piano che che sta sopra/sotto la curva, ma può essere anche dentro/fuori.
Una disequazione in due variabili è lineare se la curva che delimita la soluzione è una retta. La soluzione di una disequazione lineare è un semipiano.
Una disequazione è non lineare quando la curva che delimita la soluzione non è una retta. Può essere una parabola, una circonferenza, una funzione logaritmica o esponenziale.
ESEMPIO: risolviamo la disequazione £$y-e^x >0$£. Il primo passo è disegnare la curva che delimita la nostra soluzione. Mettiamo quindi il segno di uguaglianza e abbiamo £$y=e^x$£. Allora dobbiamo disegnare questa curva, che è la ben nota curva esponenziale. La soluzione della disequazione è data da tutti i punti le cui coordinate soddisfano £$y> e^x$£. Ma sono tutti i punti che sono “sopra" la curva. I punti della curva non fanno parte della soluzione, perché per loro vale l’uguaglianza che non è richiesta dall’esercizio. Quindi i punti della curva vanno tratteggiati in modo da segnalare che questi sono esclusi.
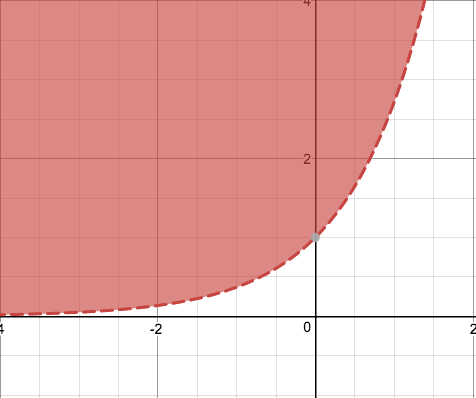
Sistemi di disequazioni in due variabili

Un sistema di disequazioni in due variabili è formato da due o più disequazioni in due variabili.
Le soluzioni del sistema è la regione di piano formata dai punti le cui coordinate verificano, contemporaneamente, tutte le disequazioni del sistema.
Graficamente, devi:
1. disegnare le curve presenti nel sistema, mettendo £$=$£ al posto del segno di disuguaglianza;
2. risolvere le singole disequazioni in due variabili;
3. considerare (o colorare se preferisci) l’intersezione delle regioni di piano. Questa sarà la soluzione del sistema.
