Funzioni numeriche particolari: proporzionalità, valore assoluto
In fisica ed in altre materie avrai sentito parlare di proporzionalità diretta, inversa e quadratica, di funzioni lineari e forse anche di valore assoluto. Sono tutte particolari funzioni numeriche con importanti applicazioni anche fuori dalla matematica! Studiamole insieme!
Impara a utilizzare le funzioni numeriche particolari, con proporzionalità tra le due variabili diretta, inversa, lineare, quadratica.
In questa video lezione imparerai:
- Proporzionalità diretta e inversa: cosa è la proporzionalità diretta e inversa e cosa sono le variabili direttamente e inversamente proporzionali
- Funzione lineare: qual è la definizione e il grafico di una funzione lineare
- Proporzionalità quadratica: qual è la definizione e il grafico di una funzione di proporzionalità quadratica
- Funzione valore assoluto: quali valori assume e come si disegna la funzione valore assoluto
- Proporzionalità diretta, inversa e quadratica
- Cos'è una funzione lineare
- Funzione valore assoluto
- Ripassa per l'interrogazione sulle funzioni particolari
- Sfida sulle proporzionalità
Proporzionalità diretta, inversa e quadratica
Proporzionalità diretta e inversa
Proporzionalità quadratica
In una funzione, £$y$£ varia al variare della £$x$£.
Se £$x$£ e £$y$£ variano mantenendo costante il loro rapporto, ovvero £$\frac{y}{x}=k$£, la funzione stabilisce tra le due variabili una proporzionalità diretta.
Le due variabili sono direttamente proporzionali e il grafico della funzione è una retta passante per l’origine (perché con £$x=0$£, avremo anche £$y=0$£ ).
Se £$x$£ e £$y$£ variano mantenendo costante il loro prodotto, £$y \cdot x=k$£, la funzione stabilisce tra le due variabili una proporzionalità inversa.
Le due variabili sono inversamente proporzionali e il grafico della funzione è un’iperbole equilatera con gli assi £$x$£ e £$y$£ come asintoti.
La funzione di proporzionalità quadratica £$y=kx^2$£, con £$k$£ costante reale (£$k \ne 0$£), ha come grafico una parabola.
Cos’è una funzione lineare
Una funzione lineare £$f(x)=mx+q$£ ha come grafico una retta, con:
- coefficiente angolare £$m$£, cioè la pendenza della retta
- quota £$q$£, cioè l’altezza alla quale la retta incontra l’asse delle ordinate (£$y$£).
Attenzione! La pendenza (£$m$£) può anche essere negativa!
Come si può ricavare il coefficiente angolare dal grafico
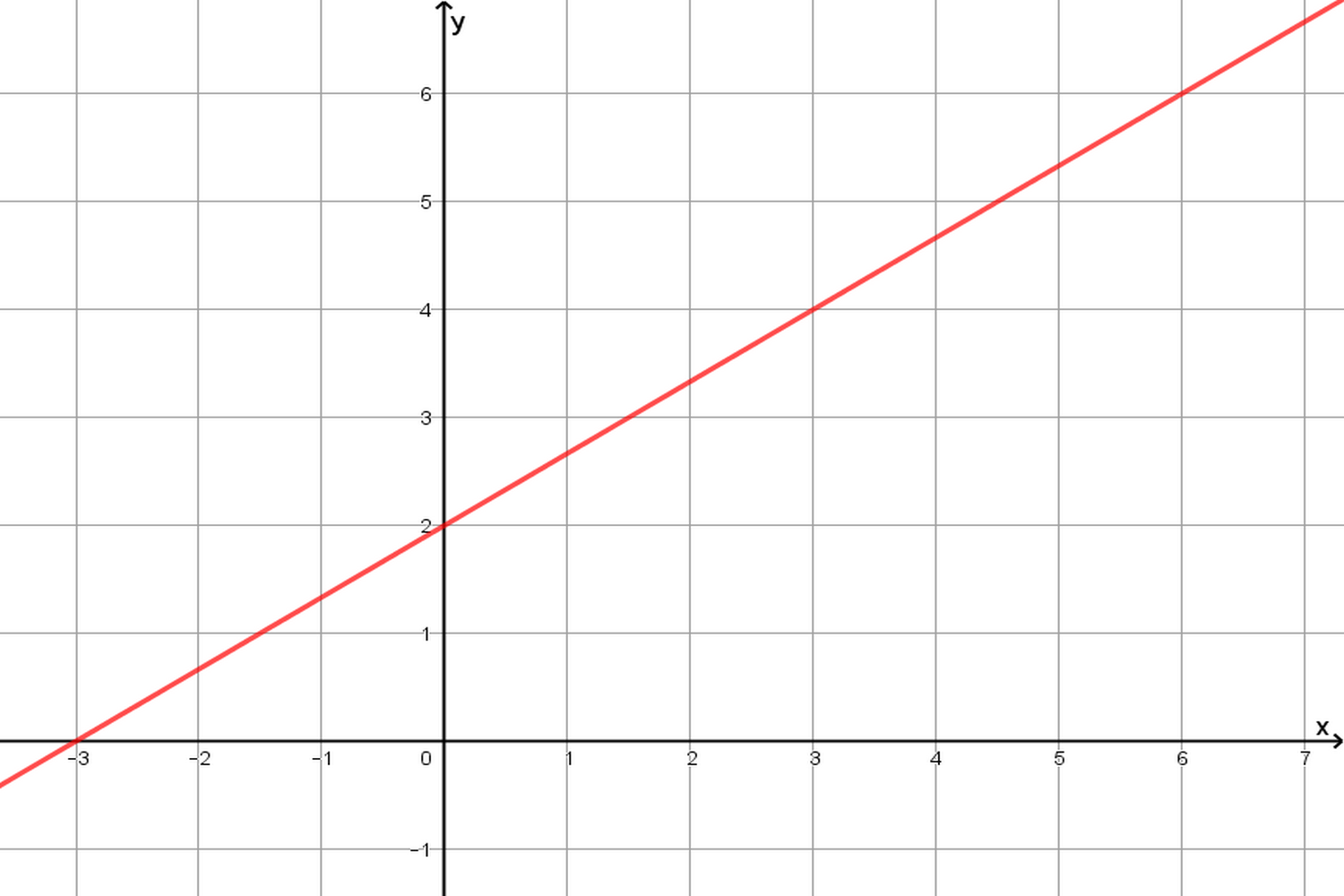
Consideriamo il primo grafico. Esso rappresenta una funzione lineare.
Sappiamo quindi che la sua equazione è del tipo: y=mx+q
L’ordinata all’origine, ovvero l’ordinata del punto di intersezione della funzione con l’asse y, è 2. Perciò l’equazione è del tipo y=mx+2
Ci resta da determinare il valore del coefficiente angolare m.
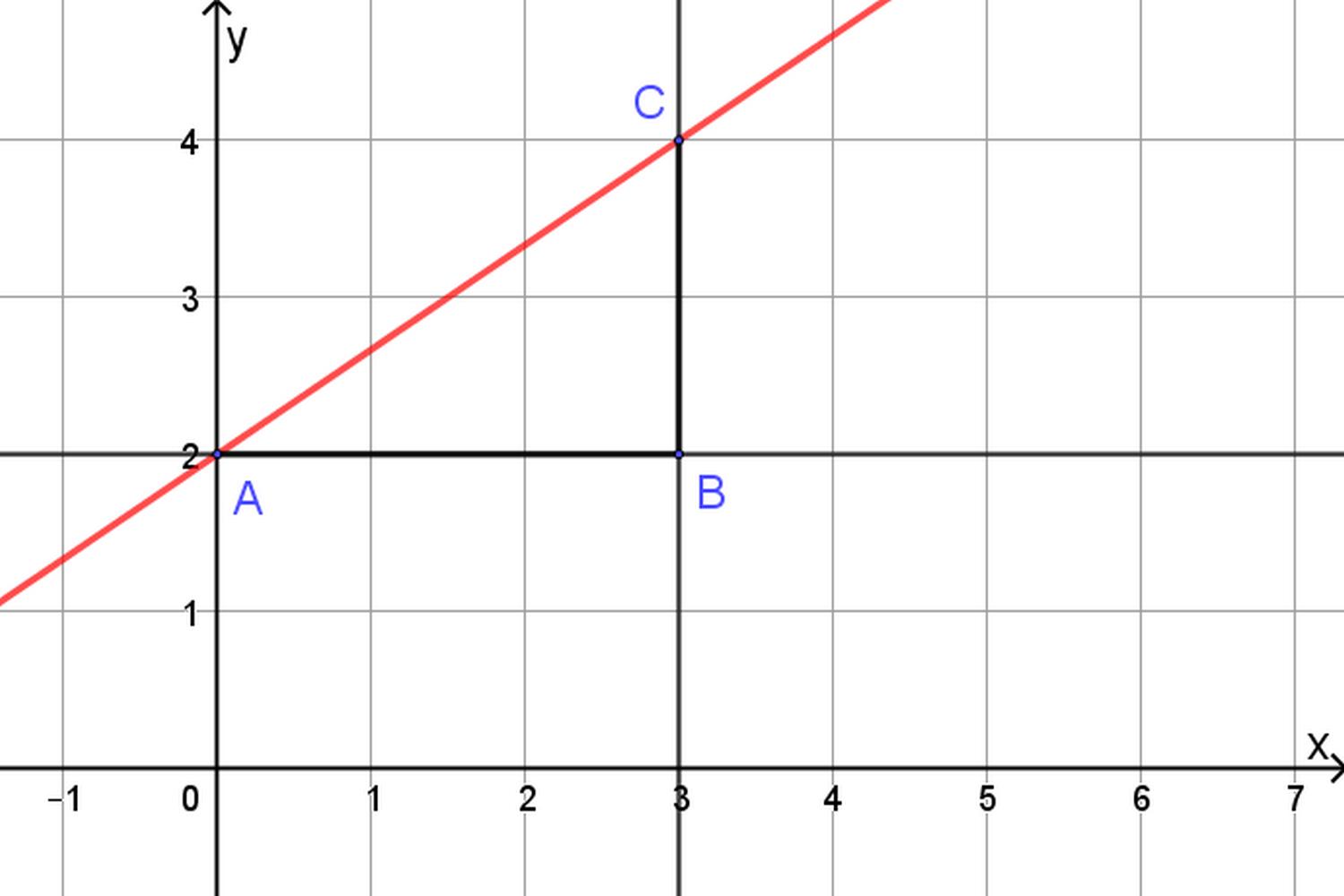
Indichiamo con A il punto di intersezione della funzione con l’asse y.
Tracciamo la retta parallela all’asse x passante per A.
Consideriamo il punto C che, come possiamo dedurre dal grafico, ha coordinate C (3;4).
Tracciamo la retta parallela all’asse y passante per C.
Il punto di intersezione tra le due rette tracciate è B, di coordinate B (3;2).
Determiniamo la lunghezza del segmento AB: £$\overline{AB}$£=3 e la lunghezza del segmento BC: £$\overline{BC}$£=2.
Il coefficiente angolare è dato dal rapporto tra le due lunghezze, in particolare:
£$m=\frac{\overline{BC}}{\overline{AB}} = \frac{2}{3}$£
Abbiamo quindi il coefficiente angolare della funzione e, di conseguenza, la sua equazione finale £$y= \frac{2}{3}x + 2$£
Non è sempre facile ricavare l’equazione della funzione lineare dal grafico, ma, in questo caso, era semplice determinare un punto C con coordinate intere e il fatto che anche l’ordinata all’origine avesse un’ordinata intera ha permesso di dedurne facilmente il valore dal grafico.
Funzione valore assoluto
La funzione £$y=\left| x \right|$£ è la funzione “valore assoluto" ed è:
- £$y=\left| x \right|=x$£ se £$ x \ge 0$£;
- £$y= \left| x \right| =-x$£ se [iol_placeholder type="formula" engine="katex" display="inline"] x
Ripassa per l’interrogazione sulle funzioni particolari
Cosa ti chiederà domani la prof nell’interrogazione?
Sai dire che cos’è una funzione numerica? Come si definisce la funzione valore assoluto? Che tipo di proporzionalità esistono?
Sfida sulle proporzionalità
Sfida:
Soluzione:
Qualunque sia la ricarica che hai fatto il mese scorso, questo mese ti verrà fatta 3 volte più grande. La funzione che rappresenta questa relazione che tipo di proporzionalità è? Prova a rispondere alla sfida e poi corri ad allenarti con gli esercizi!
