Come fare lo studio di una funzione in due variabili
Cosa sono le funzioni in due variabili? Fino ad ora hai visto le funzioni del tipo £$y=f(x)$£ cioè una variabile £$y$£ che dipende dal valore della variabile £$x$£.
Ora le variabili indipendenti sono due. Ma non ti preoccupare: tutto quello che hai imparato sulle funzioni ti servirà anche ora. Solo che adesso sarà un po’ diverso (ma anche più bello) tracciare il grafico, che sarà una superficie in tre dimensioni. Curioso di sapere come studiare le funzioni in due variabili? Potrebbe spaventare a prima vista. In realtà, valgono tutti i discorsi fatti per le funzioni in una variabile.
Beh non ha senso dirti tutto ora…scopri piano piano come studiare una funzione in due variabili e ricorda che puoi sempre allenarti con gli esercizi che sono svolti e spiegati.
- Come orientarsi in tre dimensioni
- Equazione di un piano in tre dimensioni
- Funzioni in due variabili reali
- Grafico di una funzione in due variabili
Come orientarsi in tre dimensioni
Intanto, che aspetto ha una funzione in due variabili? Beh, visto che abbiamo due variabili indipendenti, l’espressione di una funzione di questo tipo sarà £$z=f(x,y)$£
Ma cos’è £$z$£? È la variabile dipendente. Infatti in base ai valori di £$x$£ e £$y$£ (variabili indipendenti) avremo un valore della £$z$£.
Come rappresentare le funzioni in due variabili? Beh sicuramente non nel piano cartesiano, perché ora le variabili sono tre. Allora avremo bisogno di uno spazio in tre dimensioni, il cui grafico sarà quindi una superficie.
L’ambiente in cui studiare le funzioni in due variabili è lo spazio in tre dimensioni. Il sistema di riferimento cartesiano è composto da un’origine £$O$£ e da tre assi cartesiani sono £$x$£, £$y$£ e £$z$£ (perpendicolari a due a due).
PUNTI: in questo sistema di riferimento, un punto è definito da tre coordinate. L’aspetto di un punto sarà quindi £$P(x_{P};y_{P};z_{P})$£ dove le singole coordinate ci indicano la distanza dall’origine in direzione di ciascun asse, esattamente come per le funzioni in una variabile.
DISTANZA TRA DUE PUNTI: la formula per calcolare la distanza tra due punti £$P(x_{P};y_{P};z_{P})$£ e £$Q(x_{Q};y_{Q};z_{Q})$£ in tre dimensioni è la stessa usata per le due dimensioni. Ovviamente, non dobbiamo dimenticarci della terza coordinata £$z$£. Quindi la distanza tra i punti £$P$£ e £$Q$£, cioè la lunghezza del segmento £$\overline{PQ}$£ sarà
$$\overline{PQ}=\sqrt{(x_{P}-x_{Q})^2 + (y_{P}-y_{Q})^2 + (z_{P}-z_{Q})^2}$$
PUNTO MEDIO DI UN SEGMENTO: la formula per calcolare le coordinate del punto medio del segmento £$\overline{PQ}$£ è
$$x_{M}=\frac{x_{P}+x_{Q}}{2}; \quad y_{M}=\frac{y_{P}+x_{Q}}{2}; \quad z_{M}=\frac{z_{P}+z_{Q}}{2}$$
cioè come veniva calcolato in due dimensioni, con l’aggiunta della coordinata £$z$£.
Equazione di un piano in tre dimensioni
Cosa succede quando ci spostiamo in tre dimensioni? Abbiamo visto che il grafico di una funzione è una superficie. E quali sono le superficie più semplici? I piani!
L’equazione generale di un piano in tre dimensioni è £$ax+by+cz+d=0$£ con £$a,b,c,d \in \mathbb{R}$£ e non contemporaneamente nulli.
Vediamo alcuni piani particolari:
- i piani del tipo £$x=k$£ sono paralleli al piano £$yz$£, i piani £$y=k$£ sono paralleli al piano £$xz$£ mentre i piani £$z=k$£ sono paralleli al piano £$xy$£. Quindi se nell’equazione del piano compare solo una variabile, quel piano è parallelo al piano generato dalle altre due variabili.
- se nell’equazione manca una variabile, il piano è perpendicolare al piano generato dalle due variabili presenti nell’equazione ed è parallelo all’asse della variabile che manca. Ad esempio, il piano £$3x+y=0$£ è perpendicolare al piano £$xy$£ e parallelo all’asse £$z$£ mentre il piano £$y+2z+1=0$£ è perpendicolare al piano £$yz$£ e parallelo all’asse £$x$£
Come capire se due piani sono paralleli? Per prima cosa, dobbiamo guardare i coefficienti che moltiplicano le tre variabili. I coefficienti £$a,b$£ e £$c$£ sono chiamati parametri direttori del piano. Questi parametri ci permettono di identificare le direzioni del piano.
Se due piani hanno gli stessi parametri direttori allora sono paralleli. Quindi i piani £$x+y+3z=0$£ è parallelo al piano £$x+y+3z+4=0$£ perché hanno gli stessi parametri direttori.
Funzioni in due variabili reali
Le funzioni in due variabili hanno generalmente un’espressione del tipo £$z=f(x,y)$£. Cosa significa? Beh che il valore di £$z$£ dipende dai valori che hanno £$x$£ e £$y$£.
Ma che rapporto c’è tra £$x$£ e £$y$£? Queste due variabili sono indipendenti tra loro, quindi il valore di una non influisce sul valore dell’altra.
Ricorda che stiamo parlando di funzioni, quindi la prima cosa da fare è chiedersi: ma vanno bene tutti i valori oppure no? Dobbiamo calcolare il dominio della funzione. Qui valgono tutte le regole che abbiamo imparato nello studio delle funzioni in una variabile ad esempio:
- il denominatore deve essere diverso da zero
- l’argomento di una radice di indice pari deve essere maggiore o uguale a zero
- l’argomento di un logaritmo deve essere positivo
Il dominio di una funzione in due variabili è una regione (o parte) del piano. Ovviamente può essere o l’intero piano £$\mathbb{R}^2$£ oppure un suo sottoinsieme.
ESEMPIO: per calcolare il dominio della funzione £$z=\frac{x}{\ln(x+y)}$£ dobbiamo porre l’argomento del logaritmo positivo, quindi £$x+y>0$£ cioè £$y>-x$£. Ma Il logaritmo deve essere diverso da zero (perché è al denominatore). Quindi deve valere £$\ln(x+y)\ne 0 \to x+y\ne 1$£ cioè £$y\ne -x+1$£. Quindi il dominio è il semipiano sopra la retta £$y=-x$£ ma dobbiamo escludere anche la retta £$y=-x+1$£.
Grafico di una funzione in due variabili
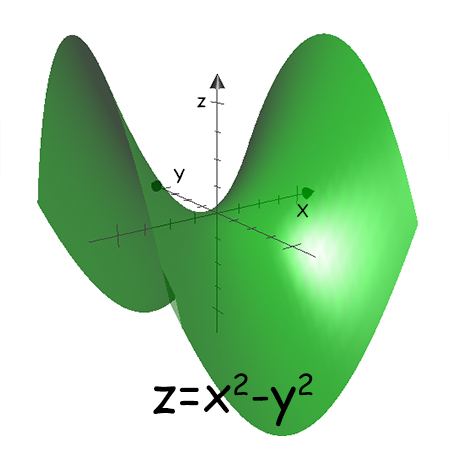
Le funzioni in due variabili sono rappresentabili nello spazio cartesiano (in tre dimensioni) con delle superfici.
Disegnare le superfici però non è affatto semplice! Infatti abbiamo bisogno di software che fanno il lavoro per noi.
Le curve di livello
Lo studio del comportamento e del grafico di una funzione a due variabili è un po’ più difficile rispetto a quello delle funzioni in una variabile. Per questo è importante studiare come è fatta la funzione a diverse “altezze". Ma cosa significa?
In pratica si tratta di “tagliare" (in matematica si dice anche intersecare) la funzione con un piano parallelo al piano £$xy$£ e vedere la curva che salta fuori. L’insieme delle curve ottenute in questo modo sono chiamate curve di livello della funzione.
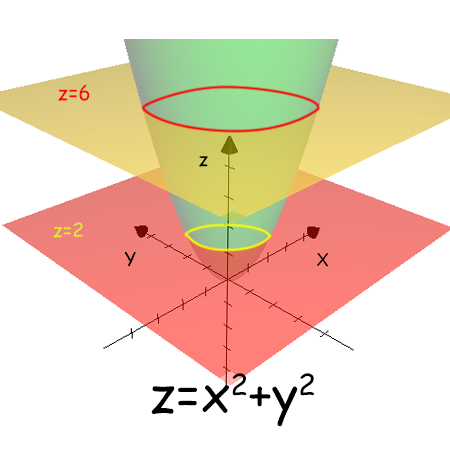
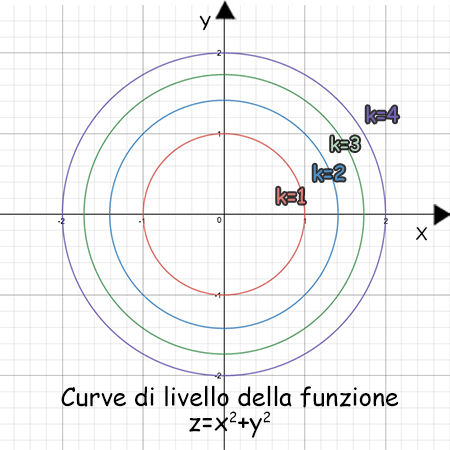
Se disegniamo (alcune) le curve di livello su un unico piano (facciamo cioè le loro proiezioni) otteniamo il grafico delle curve di livello. Questo ci permette di avere una approssimazione del grafico della funzione.
Come disegnare le curve di livello? Abbiamo detto che sono ottenute dall’intersezione tra la funzione e i piani paralleli al piano £$xy$£ che hanno equazione £$z=k$£.
Allora disegniamo le curve £$f(x,y)=k$£ al variare di £$k$£. Può essere un fascio di coniche, oppure un insieme di curve logaritmiche. Dipende tutto dall’espressione della funzione.
A cosa servono le curve di livello? Se hai presente le previsioni del tempo, sai di cosa stiamo parlando. Infatti sulla mappa vengono rappresentate le isobare, che sono delle curve che uniscono tutte le zone che si trovano alla stessa pressione oppure le isoterme, cioè quelle che sono alla stessa temperatura. In questi casi, la coordinata £$z$£ è rappresentata, rispettivamente, dalla pressione e dalla temperatura.
