I monomi: tutte le formule complete

Ti capiterà di frequente di sentir parlare di monomi e di dover affrontare equazioni, somme algebriche e potenze che li hanno come protagonisti. Ma cos’è esattamente un monomio? E come possiamo maneggiare, risolvere e comprendere espressioni che li contengono?

Un monomio, in termini semplici, è un’espressione algebrica composta una parte numerica che prende il nome di coefficiente e una parte letterale con esponenti interi e positivi. Ogni lettera, all’interno del monomio, ha un valore indipendente dalle altre: due monomi, ad esempio, possono essere definiti simili perché hanno la stessa parte letterale (cioè le lettere al loro interno sono uguali e disposte nello stesso modo), ma hanno dei coefficienti differenti. Esempi comuni includono $3x^2, 5y, 4ab$.

In questo articolo, ci dedicheremo ad andare più in profondità sui monomi, raccogliendo una serie di formule e regole che servono per risolverli e gestire espressioni che li contengono. Per tutti gli studenti in procinto di affrontare una verifica, questo articolo sarà la vostra arma segreta! Scopriremo insieme cosa sono i monomi, come si calcolano, come si svolgono le potenze dei monomi e come gestire un’espressione in cui sono presenti.

• Tabella sui monomi: tutte le formule complete
• Cosa sono i monomi
• Cos'è il grado di un monomio
• Come fare la somma algebrica dei monomi
• Come si calcola l'elevamento a potenza dei monomi
• Come calcolare il prodotto di monomi
• Come calcolare la divisione tra monomi

Tabella sui monomi: tutte le formule complete

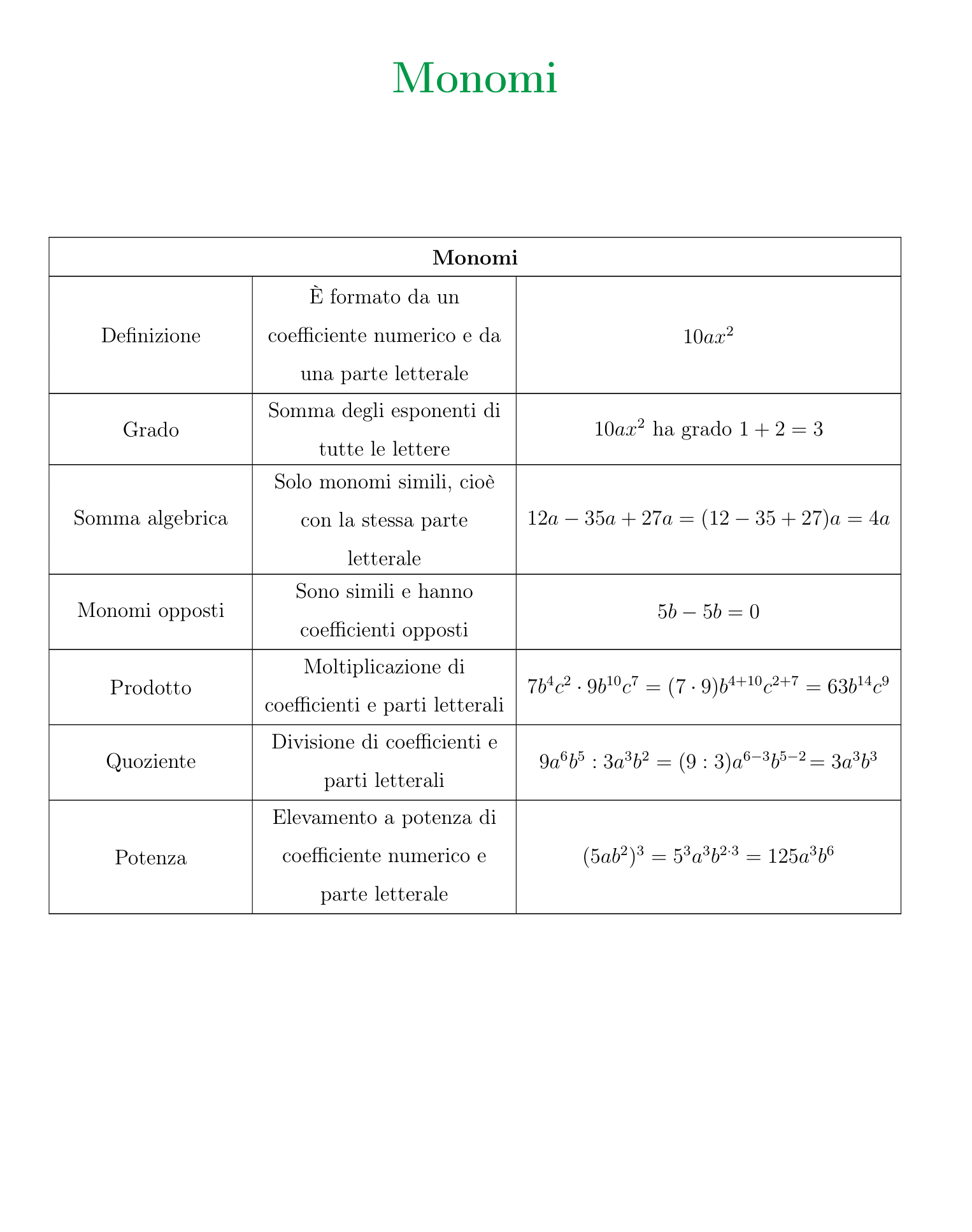
Cosa sono i monomi

Si definisce monomio ogni espressione algebrica che possiamo scrivere come prodotto di numeri e lettere. Un monomio è formato da un coefficiente numerico e una parte letterale.

Esempio: sono monomi $2xy, 5s, 10tx^2$.

Cos’è il grado di un monomio

Il grado complessivo del monomio è la somma degli esponenti di tutte le variabili che compaiono.

Il grado del monomio $a^nb^m$ è $n+m$.

Esempio: il grado del monomio $2x^5y^{10}$ è $5 + 10 = 15$.

Come fare la somma algebrica dei monomi

Possiamo sommare solo monomi simili, cioè con la stessa parte letterale. Il risultato della somma algebrica è un monomio che ha come coefficiente numerico la somma dei coefficienti, come parte letterale la stessa degli addendi.

Esempio: $12a – 35 a + 27a = (12 – 35 + 27)a = 4a$

Se due monomi simili sono opposti, allora il risultato dell’addizione è £$.

Esempio: [iol_placeholder type="formula" engine="katex" display="inline"]5b – 5b = 0$£

Come si calcola l’elevamento a potenza dei monomi

Per calcolare la potenza $n$-esima di un monomio, occorre elevare a $n$ sia coefficiente numerico sia la parte letterale.

Esempio: $(5ab^2)^3 = 5^3 a^{1·3} b^{2·3} = 125a^3b^6$

Come calcolare il prodotto di monomi

Il prodotto di due o più monomi è un monomio il cui coefficiente è il prodotto dei coefficienti, la parte letterale è il prodotto delle parti letterali.

Esempio: $7b^4c^2 · 9b^{10}c^7 = (7 · 9)b^4c^2· b^{10}c^7 =$ $63 b^{4 + 10} \cdot c^{2 + 7} = 63b^{14}c^9$

Come calcolare la divisione tra monomi

II quoziente tra due monomi è un monomio il cui coefficiente è il quoziente dei coefficienti, la parte letterale è il quoziente delle parti letterali.

Esempio: $18a^6b^5 : 9 a^3b^2 = (18 : 9) a^6b^5 : a^3b^2 =$ $2a^{6 – 3}b^{5 – 2} = 2a^3b^3$

Attenzione! Non è sempre possibile fare la divisione: se il grado di una lettera nel monomio divisore è maggiore del grado della stessa lettera nel monomio dividendo, non possiamo calcolare il quoziente.

Esempio: $18a^6b^5$ e $9 a^{13}b^2c$ non sono divisibili perché il grado di $a$ (13) e di $c$ (1) nel divisore sono maggiori del grado di $a$ (6) e di $c$ (0) nel dividendo.