Unità frazionarie e frazioni decimali: cosa sono
L’unità frazionaria rappresenta uno dei concetti fondamentali nell’ambito della matematica, in particolare quando ci addentriamo nello studio delle frazioni e della loro applicazione pratica. L’unità frazionaria è, in termini semplici, una frazione il cui numeratore è 1 e il cui denominatore è un numero intero positivo. È la rappresentazione più basilare di una frazione, esprimendo la parte di un intero diviso in parti uguali. Per esempio, se dividiamo un torta in 8 fette uguali, una singola fetta rappresenta un’unità frazionaria di quella torta, ossia 1/8.
Le frazioni decimali sono un’altra forma per esprimere le frazioni. A differenza delle frazioni comuni che utilizzano un numeratore e un denominatore per indicare le parti di un intero, le frazioni decimali si avvalgono del sistema decimale per rappresentare lo stesso concetto. Vediamo cosa sono.
- Cos'è una unità frazionaria
- Come rappresentare due frazioni
- Cosa sono le frazioni decimali
- Scheda attività - frazioni
Cos’è una unità frazionaria
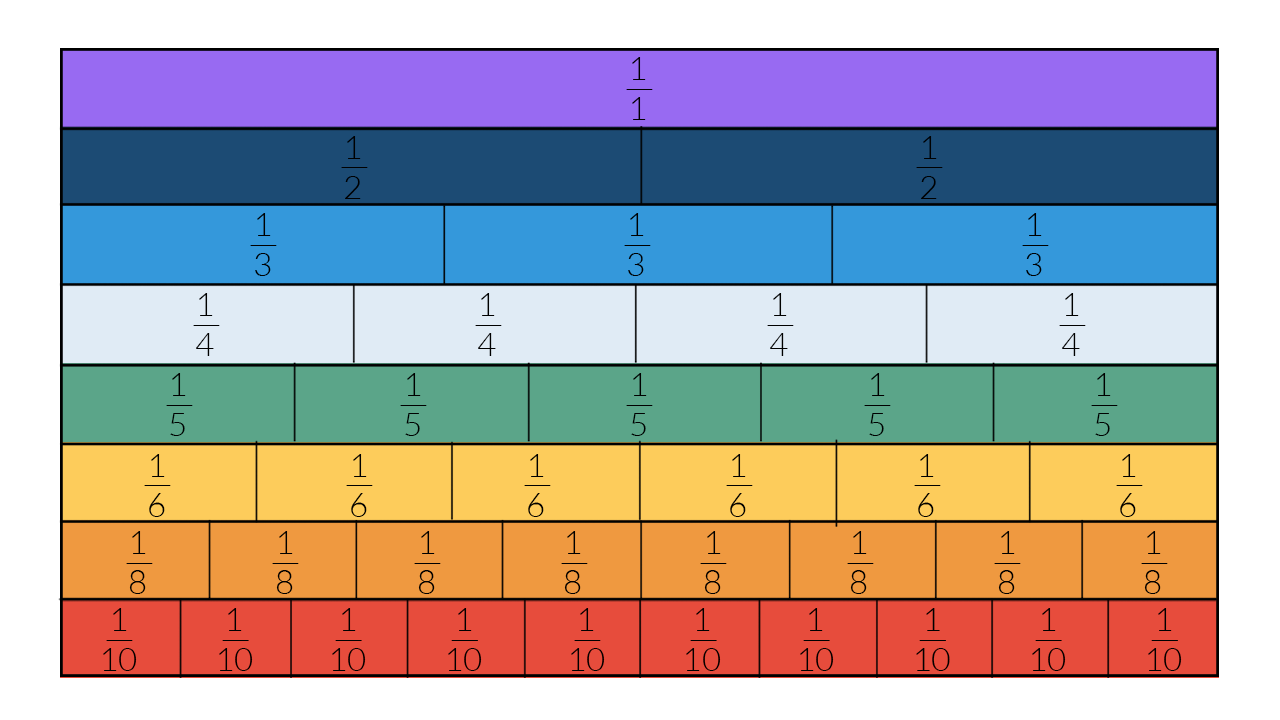
Un’unità frazionaria è una frazione che ha il numeratore uguale a 1.
L’unità frazionaria indica una parte del tutto, cioè ogni parte in cui viene diviso l’intero.
Come vediamo bene nell’immagine, più alto è il numero delle parti in cui è suddiviso l’intero, più piccola risulta essere l’unità frazionaria: più grande è il denominatore, minore è l’unità frazionaria. Prova a pensare ad una pizza: in quante fette devi dividerla per prendere una fetta grande?
Come rappresentare due frazioni

Rita ha preparato una torta e ne ha tagliate 10 fette uguali. Oscar ha mangiato 3 fette di torta, cioè ne ha mangiati i £$ \dfrac{3}{10} $£. Quanta torta rimane ancora?
Con un disegno riusciamo subito a vedere la risposta: suddividi un intero in 10 parti uguali, colora di azzurro le parti che ha mangiato Oscar. Quante parti non hai colorato? Sono quelle che avanzano!
Se Oscar ha mangiato 3 fette, significa che ne avanzano 10 – 3 = 7.
£$ \dfrac{7}{10} $£ è la frazione complementare di £$ \dfrac{3}{10} $£.
Cosa sono le frazioni decimali

Le frazioni sono numeri in cui riconosciamo un numeratore e un denominatore. Quando il denominatore è uguale a 10, parliamo di frazione decimale.
Sono frazioni decimali tutte le frazioni che hanno denominatore uguale a 10, 100 o 1000. Quando l’intero è una potenza di 10, ci troviamo di fronte a frazioni particolari: possiamo scriverle anche sotto forma di numero con la virgola, o numero decimale.
£$ \dfrac{1}{10} = 0{,}1 = $£ un decimo
£$ \dfrac{4}{100} = 0{,}04 = $£ quattro centesimi
£$ \dfrac{3}{1000} = 0{,}003 = $£ tre millesimi
Scheda attività – frazioni

In questa lezione abbiamo approfondito qualche nozione in più sulle frazioni.
Con la scheda vogliamo ripassare tutti i concetti toccati nella lezione, in particolare le unità frazionarie e le frazioni decimali. Scarica qui la scheda e scopri quale disegno è nascosto dalle frazioni: .
Un’attività interessante, può essere fatta con i LEGO.
Provate a riprodurre in classe il muro delle frazioni che abbiamo rappresentato nel primo post: scegliete il pezzo più grande come intero e poi attaccate sotto i pezzi via via più piccoli per vedere come cambiano le unità frazionarie.
