Le frazioni come divisioni e parti dell'intero
Le frazioni sono un concetto matematico fondamentale che permette di esprimere quantità che non sono intere, ma parti di un intero. Una frazione è composta da due numeri: il numeratore, che si trova sopra la linea di frazione, e il denominatore, che si trova sotto. Il denominatore indica in quante parti uguali è diviso l’intero, mentre il numeratore indica quante di queste parti stiamo considerando.
Le frazioni possono essere intese anche come una divisione tra numeri. In questo senso, il numeratore rappresenta il dividendo e il denominatore il divisore. Questa interpretazione delle frazioni come risultato di una divisione aiuta a comprendere operazioni più complesse con le frazioni, come la moltiplicazione o la divisione tra frazioni stesse.
Vediamole insieme.
Le frazioni come parte dell’intero
Rita ha preparato una torta e ha tagliato 10 fette uguali. Ognuno degli altri invitati ne mangia una fetta su 10.
La parte di torta che mangia ciascun invitato è una frazione: si scrive £$ \dfrac{1}{10} $£ e si legge “uno fratto dieci” oppure “un decimo”.
Una frazione è una parte dell’intero. Infatti frazionare significa dividere un intero in parti uguali. La frazione £$ \dfrac{1}{10} $£ ci dice che stiamo prendendo una parte delle 10 parti uguali in cui è stata suddivisa la torta.
Come leggi la frazione £$ \dfrac{2}{5} $£?
Le frazioni come divisione
Diversi modi di scrivere una frazione
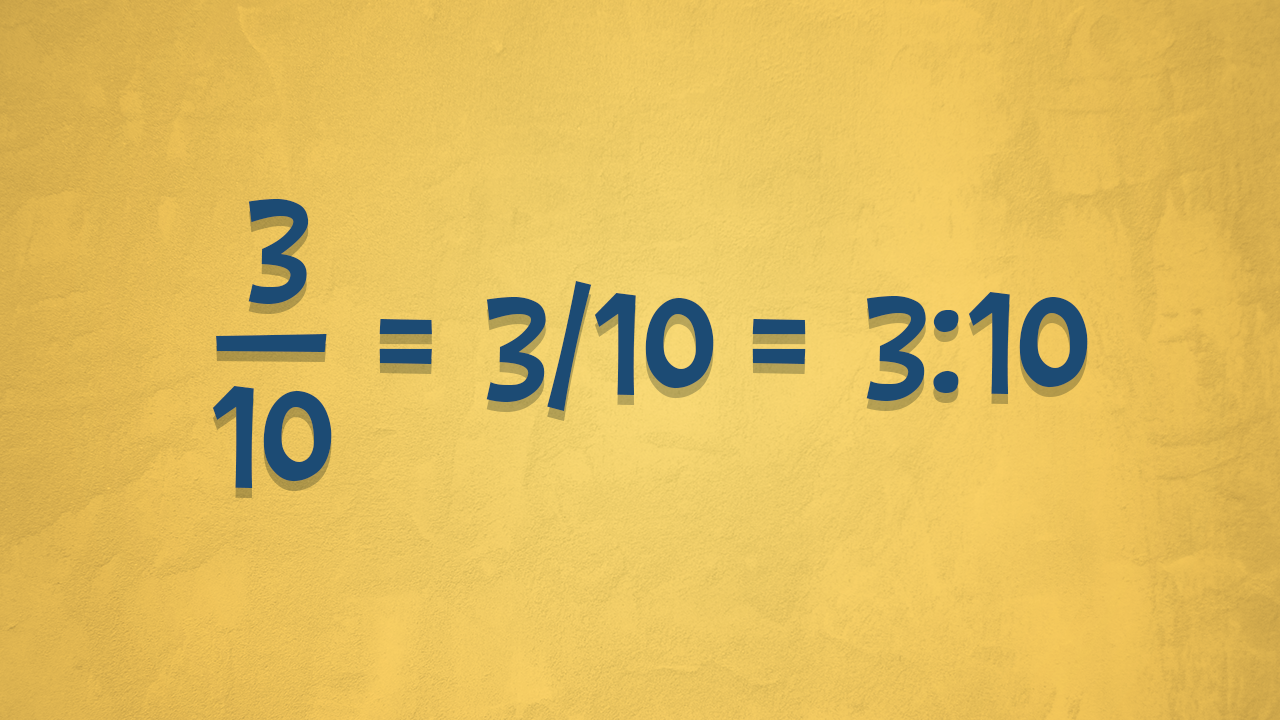
Le parti di una frazione
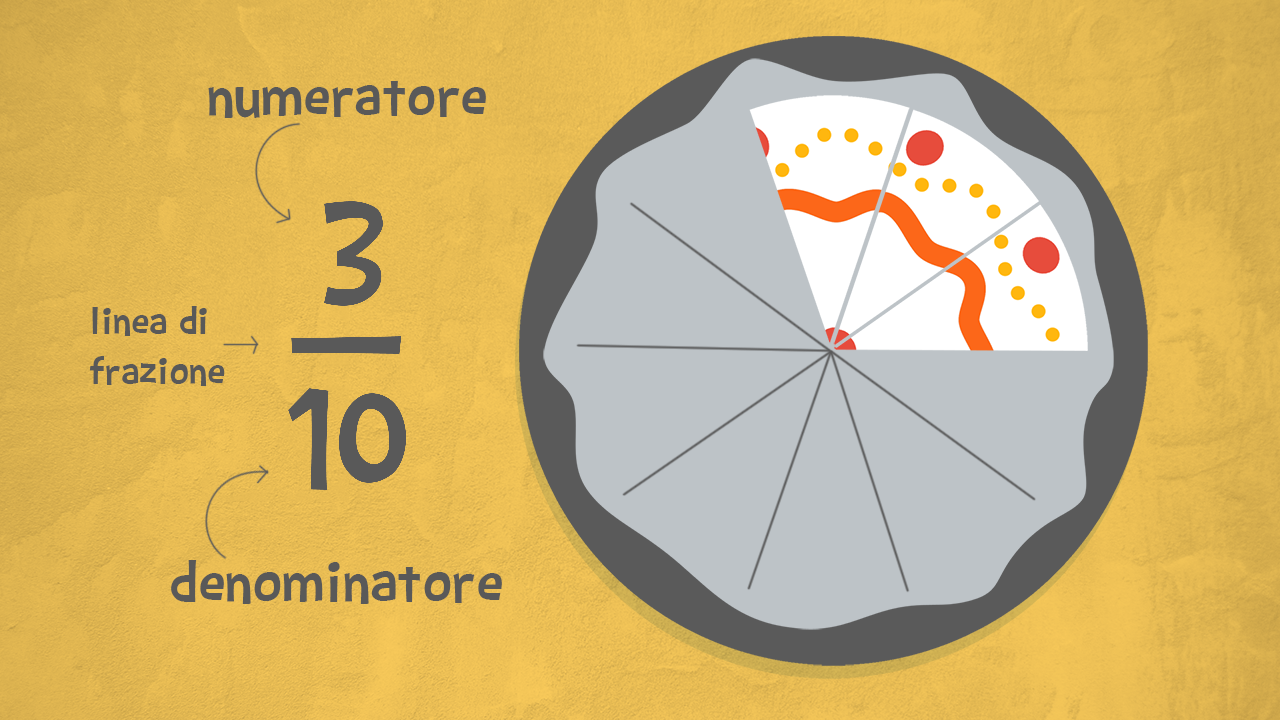
Una frazione non è altro che un numero scritto sotto forma di divisione.
Ogni volta che leggiamo o scriviamo una divisione, stiamo leggendo o scrivendo una frazione. £$ 14 : 6 $£ è una divisione. Possiamo scriverla anche così £$ 14/6 $£, oppure in verticale, come una frazione: £$ \dfrac{14}{6} $£.
Una frazione è formata da tre elementi: una linea centrale, un numero sopra e un numero sotto.
Il numero sopra alla linea è il numeratore: indica quante parti dell’intero stiamo considerando.
Il numero sotto alla linea è il denominatore: indica in quante parti uguali è suddiviso l’intero.
La linea si chiama linea di frazione e significa proprio “diviso”.
Che strane queste frazioni…
Abbiamo imparato che le frazioni sono divisioni, ma sono anche parti di un intero. Infatti, leggiamo più frequentemente frazioni in cui il numeratore è minore del denominatore.
Come si risolvono quelle divisioni in cui il dividendo è più piccolo del divisore? Impossibile, dici? Non è così. Il risultato che otteniamo sarà più piccolo di 1, ma non si tratta di una divisione impossibile. Lo imparerai presto studiando i numeri decimali e i loro legami con le frazioni (dai un’occhiata alle nostre lezioni qui).
Esercizi sulle frazioni
Frazione sì o frazione no?
Con le frazioni i bambini imparano un nuovo modo di scrivere una divisione. I concetti più importanti di questa lezione sono due:
- le frazioni sono un modo diverso di scrivere una divisione;
- frazionare un intero significa dividerlo in parti uguali.
Iniziamo con una scheda che insiste proprio su questo fatto: le parti in cui è suddiviso l’intero devono essere tutte uguali, altrimenti non possiamo parlare di frazione. Scarica qui la prima scheda: .
Proponiamo un gioco per divertirsi un po’ con le frazioni: ogni alunno, lanciando un dado, sceglie quale frazione colorare nella colonna corrispondente al risultato del dado. Il gioco continua finché tutte le frazioni nella tabella saranno colorate. Altrimenti i ragazzi si possono sfidare a coppie: vince chi riesce a colorare cinque frazioni in una riga. Scaricate qui la scheda da stampare: .
Prendiamo confidenza con le frazioni: osservate una tessera del domino, non sembra proprio una frazione? Se la giriamo in verticale, abbiamo due numeri separati da una linea orizzontale: sono il numeratore, il denominatore e la linea di frazione. Rimuovete le tessere che non hanno numeri (per evitare di dividere per 0) e sfidate gli alunni a leggere correttamente ciascuna frazione. Buon divertimento!
Lancia il dado e colora
