Frazioni complementari e equivalenti: come distinguerle
Le frazioni complementari e le frazioni equivalenti sono due concetti molto importanti da sviluppare. Le frazioni complementari si riferiscono a coppie di frazioni che, quando sommate, danno come risultato un intero. In altre parole, se abbiamo una frazione che rappresenta una parte di un intero, la sua frazione complementare rappresenta la parte restante dell’intero. Per esempio, se consideriamo la frazione £$\frac14$£, la sua frazione complementare è £$\frac34$£, poiché la somma di £$\frac14$£ e £$\frac34$£ è 1, o l’intero completo. Il concetto di frazioni complementari è particolarmente utile in situazioni che richiedono la divisione o la distribuzione equa di risorse, consentendo una facile visualizzazione di come le parti si combinano per formare un tutto.
D’altra parte, le frazioni equivalenti sono frazioni diverse che rappresentano lo stesso valore o la stessa proporzione dell’intero. Questo significa che, nonostante le differenze nei loro numeratori e denominatori, queste frazioni indicano la stessa parte di un intero quando ridotte alla loro forma più semplice. Ad esempio, le frazioni £$\frac24, \frac36,\frac 48$£ sono tutte equivalenti, poiché tutte si semplificano in £$\frac12$£ quando ridotte ai minimi termini. La comprensione delle frazioni equivalenti è fondamentale per la manipolazione e la semplificazione delle frazioni, oltre che per la risoluzione di problemi che coinvolgono le proporzioni e i rapporti.
Vediamole nel dettaglio.
Frazioni complementari
Due frazioni sono complementari se una completa l’altra.
Cosa vuol dire completare una frazione? Una frazione indica una parte dell’intero: la sua complementare è la frazione che indica quanto manca per arrivare all’intero.
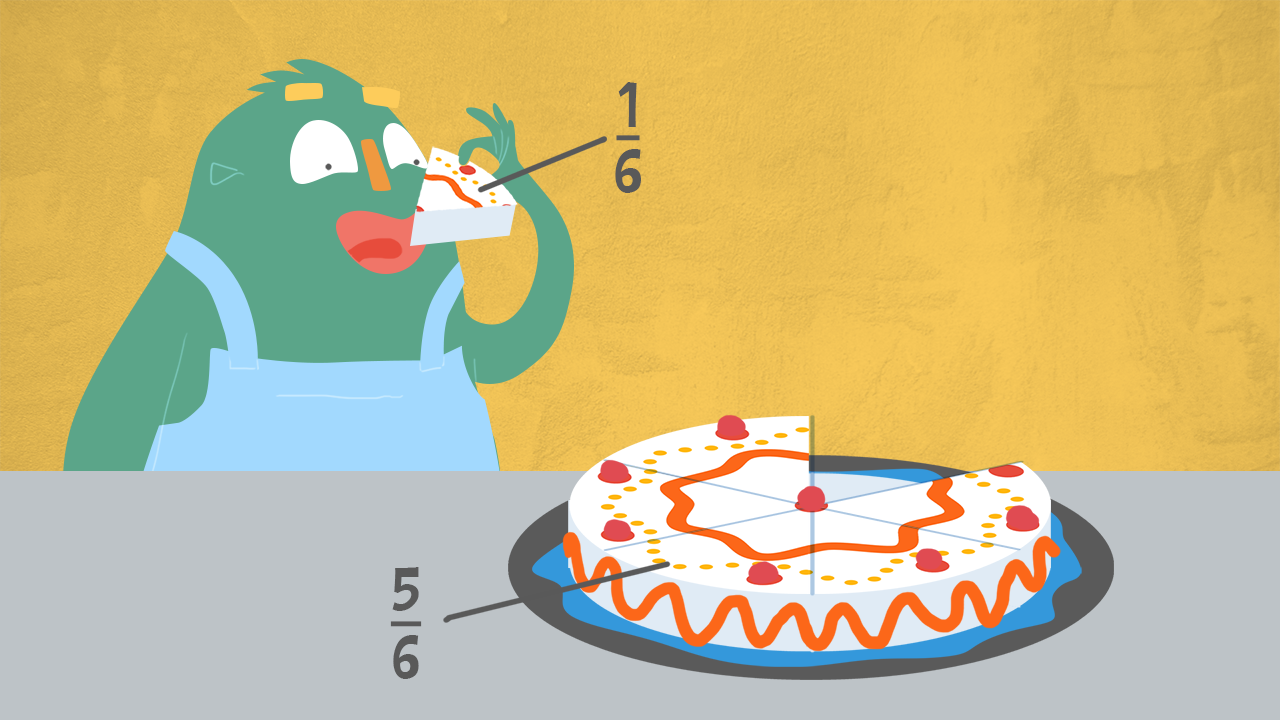
Esempio: £$ \dfrac{5}{6} $£ e £$ \dfrac{1}{6} $£ sono complementari.
Le frazioni complementari sono quelle frazioni che, sommate, danno l’intero.
Se Oscar mangia prima una fetta, poi altre cinque fette di quella torta… se l’è mangiata tutta!
Frazioni equivalenti
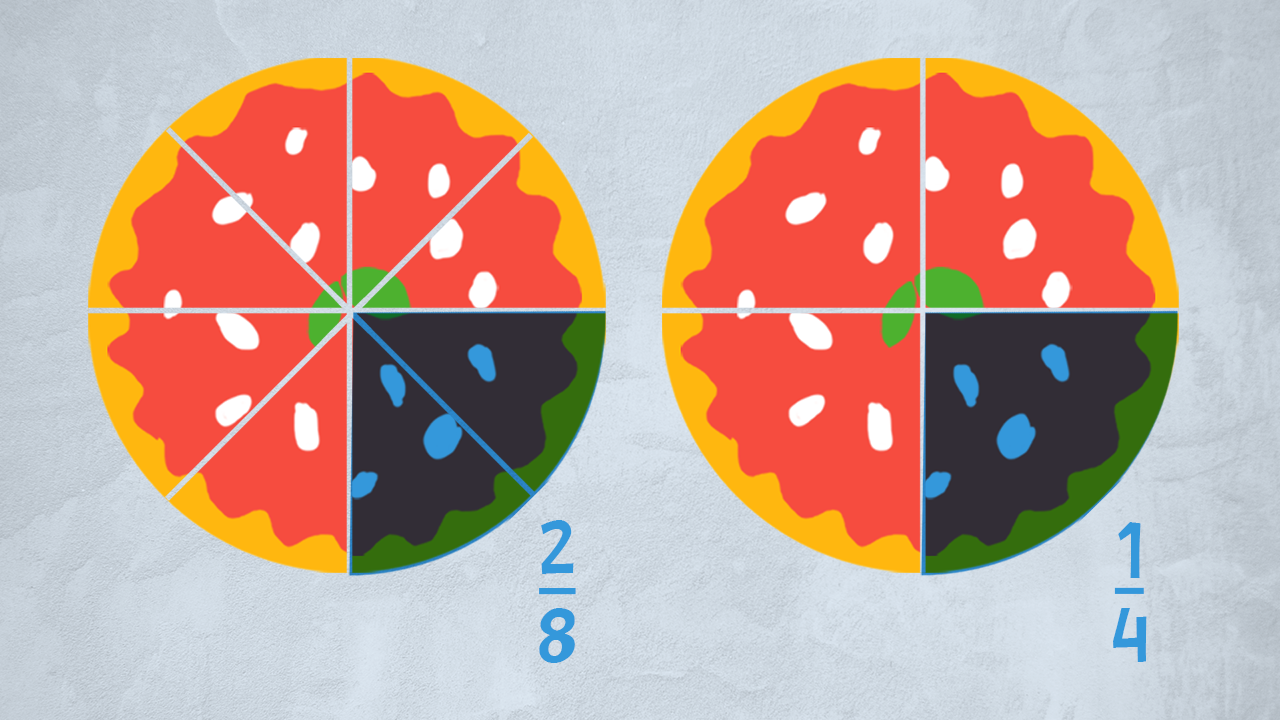
Le frazioni equivalenti sono quelle frazioni che indicano la stessa quantità, la stessa parte dell’intero.
Possiamo dividere l’intero in parti uguali, in diverso numero: consideriamo un intero e frazionato in 8 parti, poi lo stesso intero frazionato in 4 parti. Quante parti devo prendere da una parte e dall’altra per ottenere la stessa quantità?
Aiutiamoci sempre con le nostre torte: dividere una torta in 8 parti uguali, significa farne 8 fette tutte uguali. Dividerla in 4 parti uguali, invece, significa dividerla in fette che sono grosse il doppio delle 8 di prima. Mangiare una fetta della seconda torta equivale a mangiarne due della prima torta.
Infatti se consideriamo le frazioni £$ \dfrac 14 $£ e £$ \dfrac 28 $£, vediamo che il numeratore e il denominatore della seconda sono il doppio rispetto a quelli della prima frazione.
Esercizi da svolgere sulle frazioni
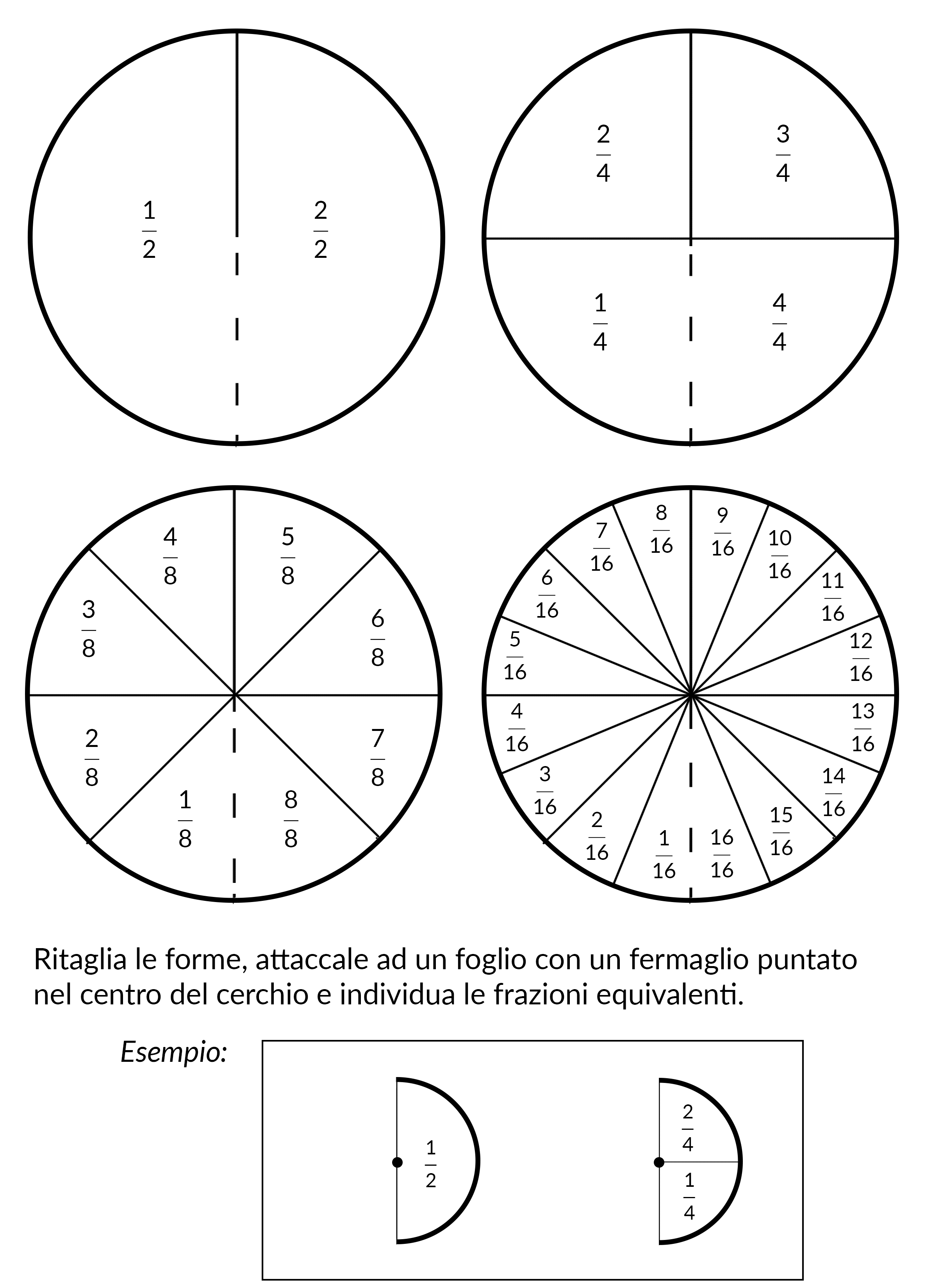
Le frazioni sono dei numeri scritti in forma di divisione. Come tutti i numeri, indicano una quantità, quindi due frazioni diverse possono indicare la stessa quantità! Vi proponiamo un’attività per verificare con mano quali sono le frazioni equivalenti. Scarica tutto il necessario per giocare con le frazioni equivalenti: .
Questo è solo un esempio, sbizzarritevi con altre forme e frazioni!
Con questa attività potrete far notare di volta in volta che frazioni equivalenti hanno numeratore e denominatore in proporzione: i bambini si accorgeranno che, prese due frazioni equivalenti, se per passare dal numeratore della prima a quello della seconda devo moltiplicare (o dividere) per un numero £$ n $£, dovrò moltiplicare (o dividere) per quello stesso numero £$ n $£ anche per passare da un denominatore all’altro.
