Come confrontare frazioni con stesso denominatore o numeratore
Oggi parliamo di un argomento molto interessante e utile nella matematica: le frazioni. Le frazioni sono un modo per rappresentare parti di un intero, proprio come quando dividiamo una pizza in fette. Ci concentreremo su due tipi speciali di frazioni: quelle con lo stesso denominatore e quelle con lo stesso numeratore.
Come si fa a sapere quale frazione è più grande rispetto ad un’altra? Basta fare un confronto! Scopri come confrontare due frazioni quando hanno lo stesso denominatore o lo stesso numeratore, impara qualche trucchetto e diventa un asso delle frazioni!
Qual è più grande? Qual è più piccola? Impara tutti i trucchi per confrontare le frazioni!
- Qual è la frazione più grande?
- Come confrontare due frazioni con lo stesso denominatore
- Come confrontare due frazioni con lo stesso numeratore
- Un trucco per confrontare le frazioni
- Scheda didattica per il ripasso delle frazioni
Qual è la frazione più grande?

Abbiamo imparato a confrontare i numeri riconoscendo il più piccolo e il più grande.
Possiamo anche confrontare le frazioni? Certamente sì!
Sappiamo che le frazioni indicano una parte dell’intero, quindi dobbiamo imparare come riconoscere quella frazione che indica la parte più grande dell’intero.
PS: serve per non rimanere fregati al momento della spartizione di una pizza! 😉
Come confrontare due frazioni con lo stesso denominatore
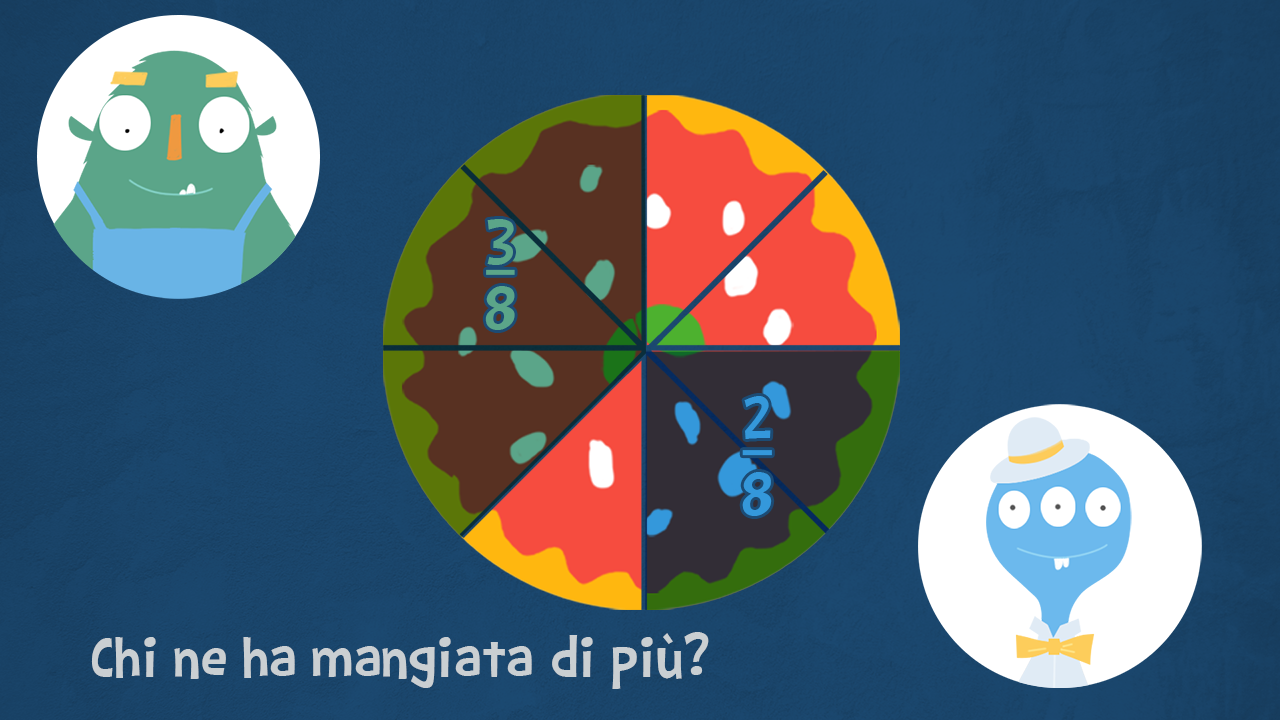
La pizza preparata da Rita per la merenda è suddivisa in 8 fette. Oscar ne ha mangiati i £$ \dfrac 38 $£, mentre Albert ne ha mangiati i £$ \dfrac 28 $£. Chi dei due ne ha mangiata di più?
Quando siamo di fronte a due frazioni che hanno lo stesso denominatore, non è difficile capire qual è la più grande.
L’intero è diviso in uno stesso numero di parti: la frazione maggiore è quella che ne considera di più, quindi quella che ha il numeratore più grande!
Come al solito, è Oscar il mangione di turno!
Come confrontare due frazioni con lo stesso numeratore
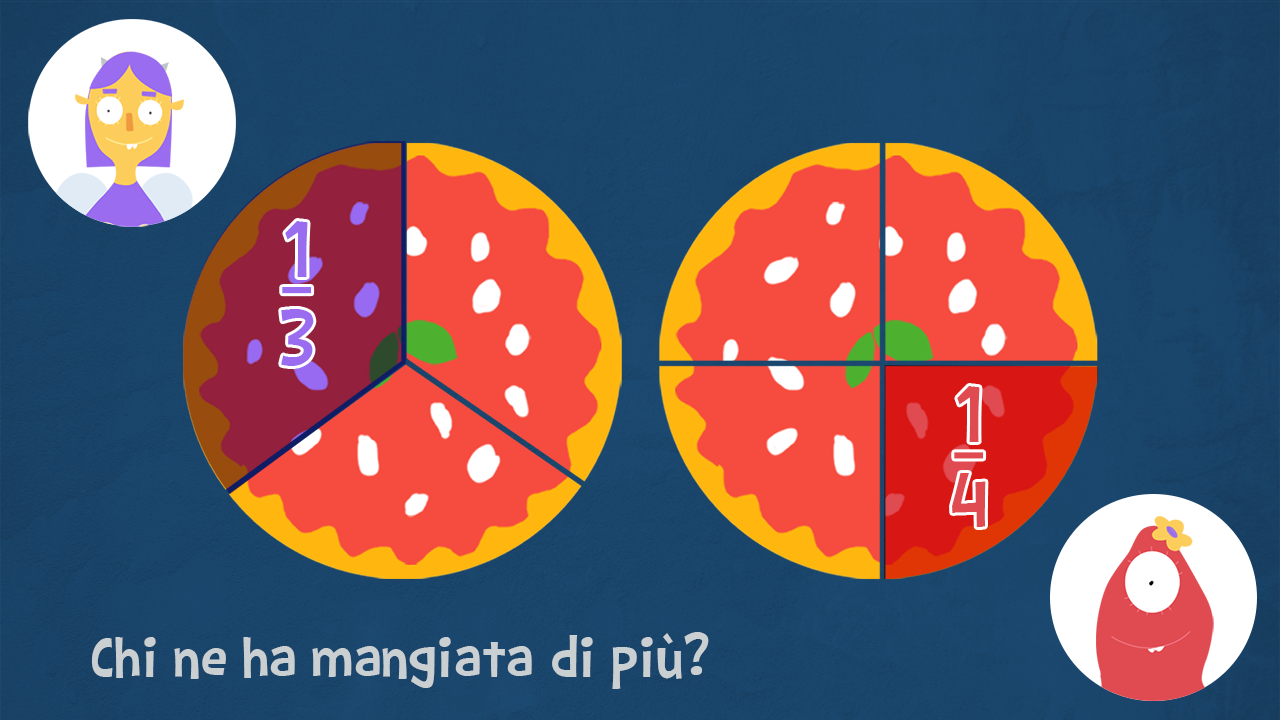
Lisa mangia £$ \dfrac 13 $£ di pizza, mentre Rita ne mangia £$ \dfrac 14 $£. Chi delle due ne ha mangiata di più?
Siamo di fronte a due frazioni che hanno lo stesso numeratore: ciò significa che abbiamo considerato lo stesso numero di parti di un intero, in questo caso 1. Dobbiamo quindi controllare in quante parti è stato suddiviso l’intero: più è grande il denominatore, più sono le parti in cui è stato suddiviso l’intero, di conseguenza le fette di pizza saranno più piccole.
In questo caso, la frazione maggiore è quella che ha il denominatore più piccolo.
Un trucco per confrontare le frazioni
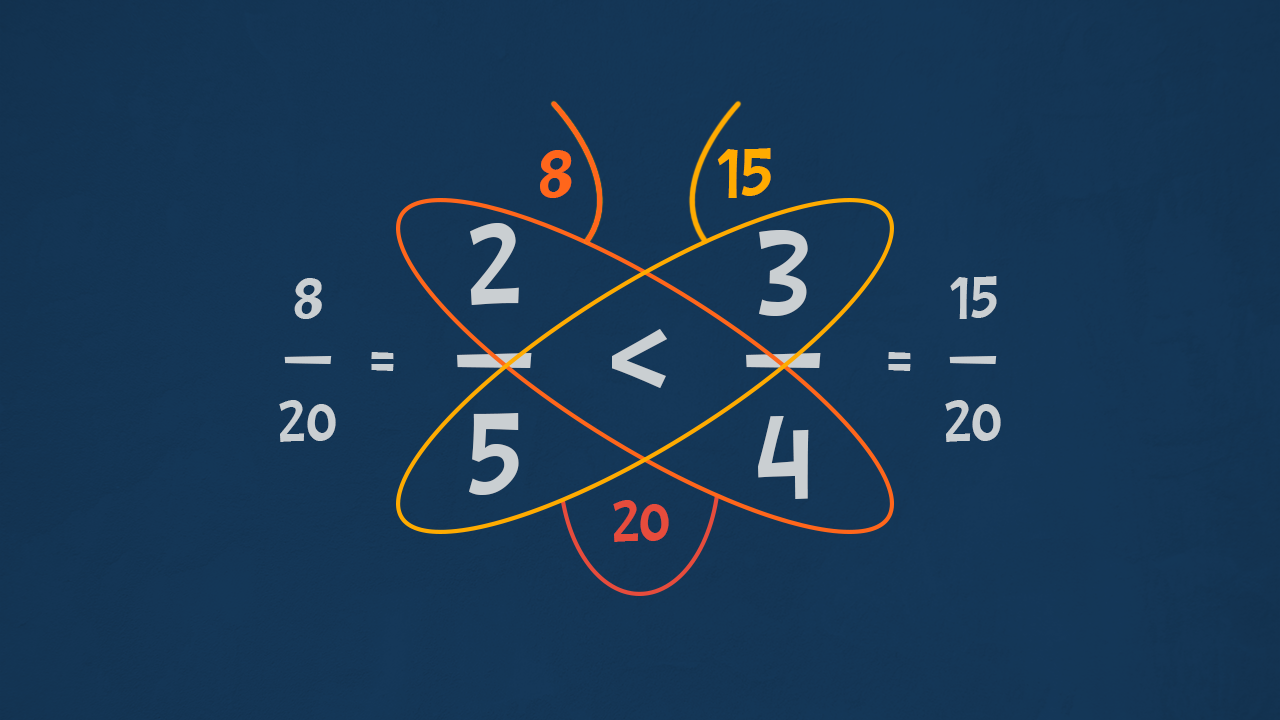
C’è un trucco per trovare subito la frazione più grande in casi generali: il trucco della farfalla!
Per trovare la più grande tra due frazioni qualsiasi, ci basta fare una moltiplicazione tra il numeratore della prima ed il denominatore della seconda e viceversa, quindi confrontare i risultati. Quella che disegniamo è proprio una farfalla!
Proviamo a confrontare le due frazioni £$ \dfrac 34 $£ e £$ \dfrac 23 $£ con questo metodo:
- dal prodotto tra il numeratore della prima ed il denominatore della seconda troviamo 3 x 3 = 9;
- facciamo quindi il prodotto tra il numeratore della seconda ed il denominatore della prima, troviamo 2 x 4 = 8;
- poiché 9 è più grande di 8, possiamo dire che £$ \dfrac 34 $£ è maggiore di £$ \dfrac 23 $£.
Di fatto abbiamo trasformato le due frazioni in modo che abbiano lo stesso denominatore, uguale al prodotto dei due denominatori: 4 x 3 = 12. Ci riconduciamo al primo caso che abbiamo analizzato, e capiamo subito che £$ \dfrac{9}{12} > \dfrac{8}{12} $£.
Abbiamo risolto il nostro problema: £$ \dfrac 34 > \dfrac 23 $£.
Scheda didattica per il ripasso delle frazioni
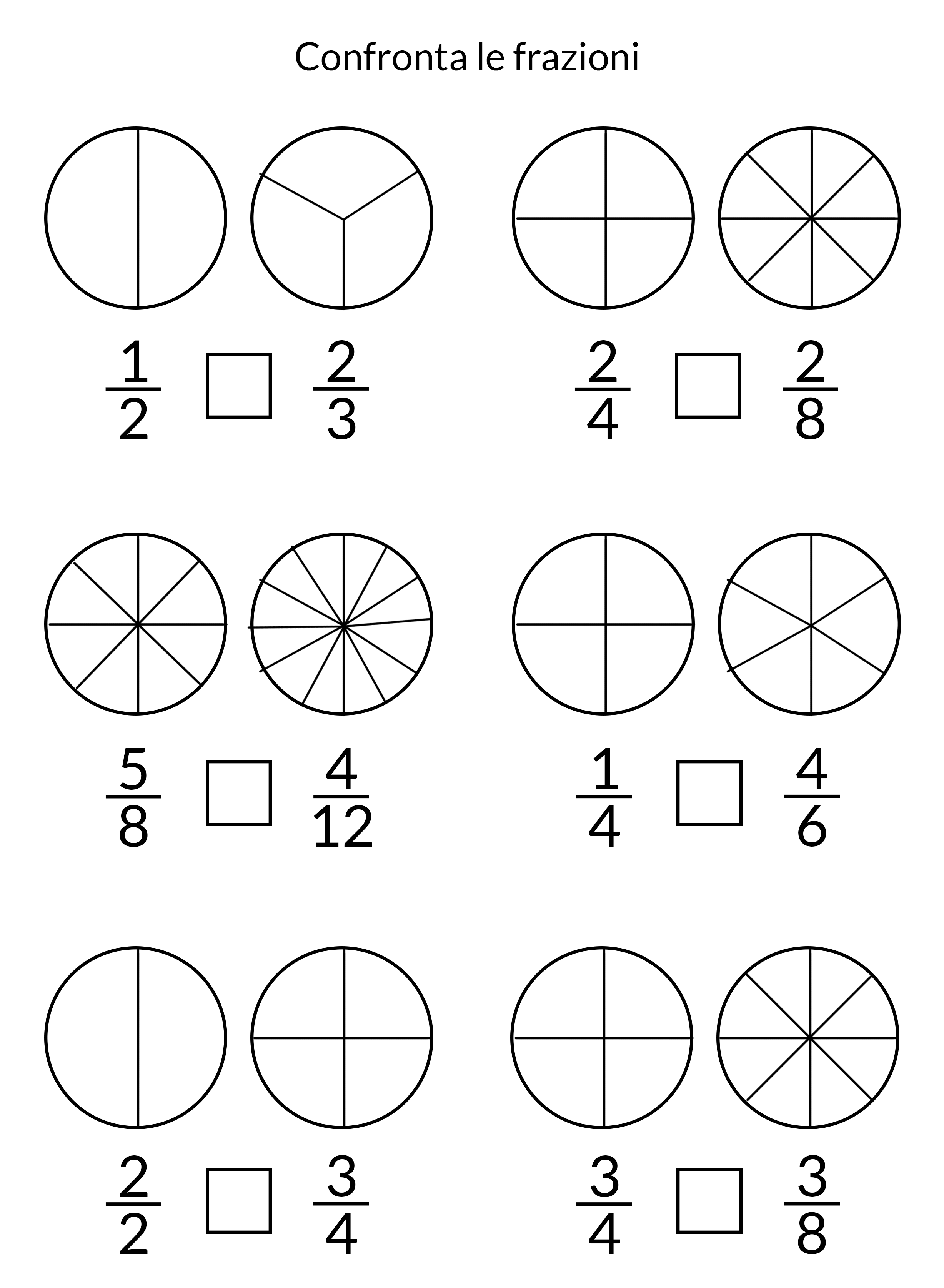
Non è sempre facile capire quale frazione è maggiore di un’altra. Nella nostra scheda proponiamo qualche semplice esercizio per prendere confidenza con le tre regole che abbiamo imparato nella lezione.
Scaricala la scheda qui:
Con l’aiuto delle nostre carte, possiamo fare un gioco: la guerra delle frazioni!
Occorrono delle matite (serviranno come linea di frazione) e un mazzo di carte senza le figure e i jolly. Distribuite le carte ai partecipanti che le radunano in un mazzetto che posizionano a faccia in giù. In ciascun turno, i due sfidanti pescano le prime due carte dal mazzo, ne posizionano una sopra e una sotto alla linea di frazione, quindi le girano contemporaneamente. Confrontano le due frazioni che si sono formate e decidono qual è la maggiore: il giocatore che ha composto la frazione più grande prende tutte e quattro le carte. Vince chi è riuscito a prendere il maggior numero di carte.
Possiamo anche dare un valore alle figure invece di rimuoverle dal mazzo: il fante vale 11, la donna vale 12 e il re vale 13. Per aumentare ancora di più la difficoltà, invece, possiamo aggiungere i jolly e le figure con la funzione vera e propria di jolly: i bambini potranno decidere quanto far valere queste carte che usciranno al numeratore o al denominatore in modo da riuscire a conquistare le carte in tavola.
Non ci resta che augurarvi buon divertimento!
