Problema da svolgere con i solidi di rotazione
Un solido di rotazione si ottiene ruotando una figura bidimensionale, come un rettangolo o un triangolo, attorno a una linea fissa chiamata asse di rotazione. Immaginate di prendere, ad esempio, un semplice rettangolo e di farlo ruotare attorno a uno dei suoi lati: il risultato sarebbe un cilindro, una delle forme più elementari e riconoscibili tra i solidi di rotazione. Allo stesso modo, facendo ruotare un triangolo attorno a uno dei suoi lati, si otterrebbe un cono, un’altra figura familiare che dimostra la varietà di forme che possono emergere da questo processo.
Queste figure sono onnipresenti nella vita quotidiana e nella tecnologia, dai semplici contenitori e ruote agli oggetti più complessi come turbine, eliche e componenti di macchinari. Proviamo ad esercitarci insieme con un problema matematico che abbia come protagonista un solido di rotazione.
- Testo del problema con un solido di rotazione
- Soluzione del punto a)
- Soluzione del punto d)
- Soluzione del punto h)
Testo del problema con un solido di rotazione
Un rettangolo ha la base che misura £$ 2 \text{ m} $£ e la sua altezza misura £$ 5 \text{ m} $£.
a) Calcola l’area del rettangolo.
b) Ora assumi come asse di rotazione la retta che passa per l’altezza del rettangolo e fallo ruotare di 360° attorno ad essa. Che solido hai ottenuto?
c) Questo solido nella realtà corrisponde ad una cisterna per il carburante di una azienda di autotrasporti. Calcola la superficie laterale della cisterna.
d) Sulla cisterna viene collocato un grande cartello con scritto LIQUIDO INFIAMMABILE la cui superficie è £$ \dfrac 15 $£ della superficie laterale; sapendo che la base del cartello misura £$ 4 \text{ m} $£, calcola quanto è alto.
e) Calcola ora il volume della cisterna.
f) La cisterna viene riempita completamente con gasolio per autotrazione. Calcola quanti litri di gasolio può contenere.
g) Calcola il peso del carburante contenuto nel serbatoio, sapendo che il gasolio ha peso specifico (densità) di £$ 0,8 \text{ kg}/\text{dm}^3$£.
h) L’azienda possiede numerosi camion. Se il serbatoio di ciascuno di essi può contenere fino a £$400$£ litri di gasolio, quanti pieni è possibile ottenere utilizzando tutto il contenuto della cisterna?
Soluzione del punto a)
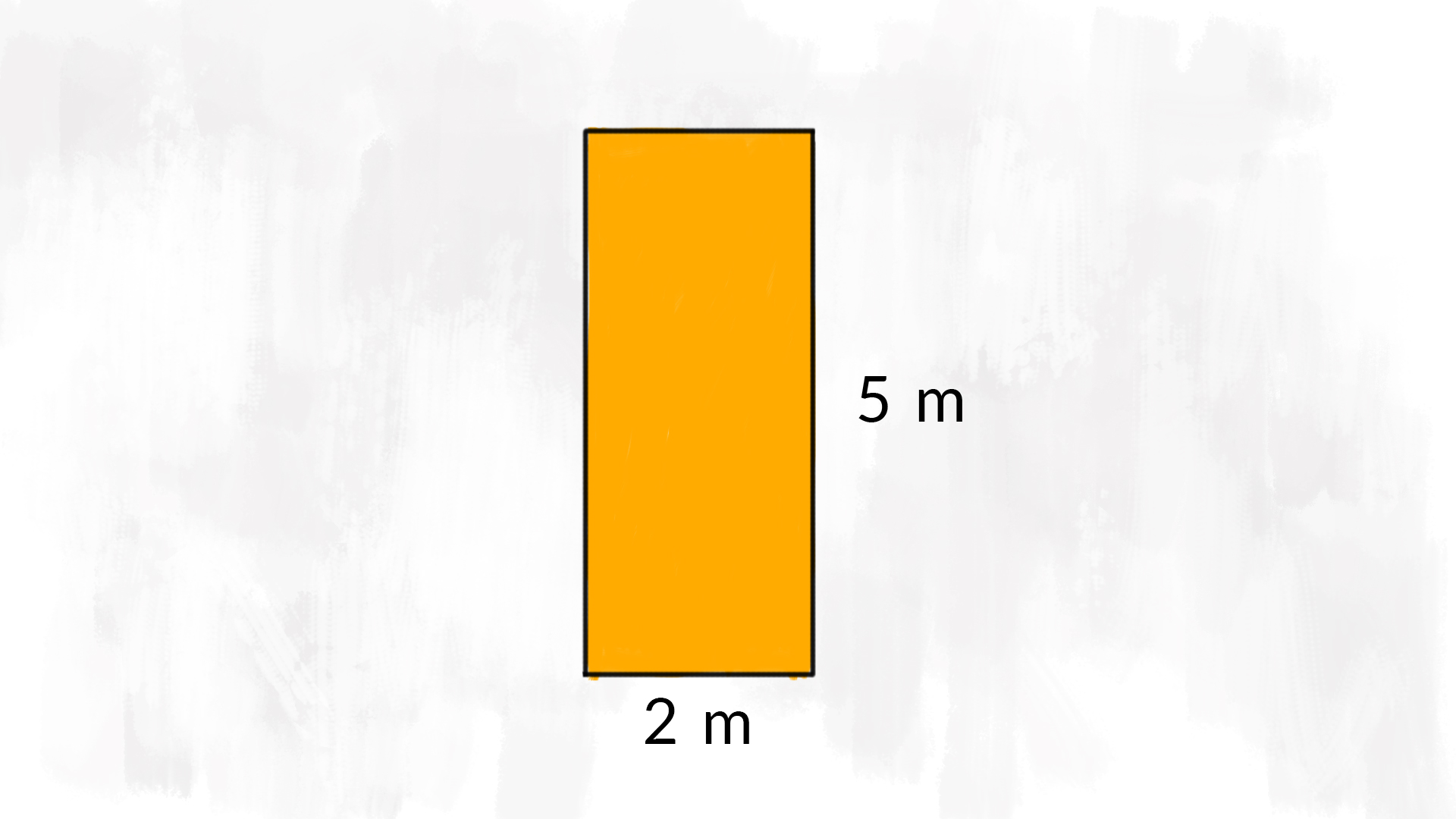
Un rettangolo ha la base che misura £$ 2 \text{ m} $£ e la sua altezza misura £$ 5 \text{ m} $£.
a) Calcola l’area del rettangolo.
Disegniamo il rettangolo. Calcolare l’area è semplice: basta moltiplicare la base per l’altezza.
$$ A = 2 \cdot 5 = 10 \text{ m}^2 $$
Soluzione del punto d)

d) Sulla cisterna viene collocato un grande cartello con scritto LIQUIDO INFIAMMABILE la cui superficie è £$ \dfrac 15 $£ della superficie laterale; sapendo che la base del cartello misura £$ 4 \text{ m} $£, calcola quanto è alto.
Il cartello è rettangolare. La sua superficie misura £$ \dfrac 15 \cdot 62,8 = 12,56 \text{ m}^2 $£. Sappiamo poi che la base del rettangolo è di £$ 4 \text{ m} $£, quindi troviamo facilmente la sua altezza:
$$ \text{altezza cartello} = \frac{12,56}{4} = 3,14 \text{ m} $$
Soluzione del punto h)
h) L’azienda possiede numerosi camion. Se il serbatoio di ciascuno di essi può contenere fino a £$400$£ litri di gasolio, quanti pieni è possibile ottenere utilizzando tutto il contenuto della cisterna?
Per rispondere a questa ultima domanda, ci basta fare una divisione. Dividiamo la quantità totale di gasolio per la capacità dei camion:
$$ 62 \, 800 : 400 = 157 $$
Utilizzando tutto il contenuto della cisterna, è possibile ottenere £$ 157 $£ pieni di gasolio per i camion dell’azienda.
