Gli integrali impropri di prima, seconda e terza specie
Gli integrali impropri sono concetti fondamentali nell’analisi matematica, particolarmente importanti per comprendere il comportamento delle funzioni su intervalli infiniti o su funzioni che presentano punti di discontinuità.
Tra questi, spiccano gli integrali di prima, seconda e terza specie, ciascuno con caratteristiche e applicazioni specifiche. In questo articolo vedremo in dettaglio cosa sono, come vengono calcolati e quali sono le loro proprietà distintive.
Impara a risolvere un integrale improprio ricorrendo ai limiti e tramite gli esercizi svolti. Capisci quando un integrale improprio è convergente, divergente o indeterminato.
In questa lezione imparerai:
- di che tipo è l’integrale improprio di prima specie e formula risolutiva
- di che tipo è l’integrale improprio di seconda specie e formula risolutiva
- di che tipo è l’integrale improprio di terza specie e formula risolutiva
- Definizione di integrale improprio
- Integrale improprio di prima specie
- Integrale improprio di seconda specie
- Integrale improprio di terza specie
- Esercizi sugli integrali impropri
- Sfida sugli integrali impropri
Definizione di integrale improprio
Un integrale è improprio quando nell’intervallo di integrazione ci sono degli infiniti o dei punti di discontinuità della funzione. In questi casi calcoliamo l’integrale ricorrendo al calcolo di un limite.
Può accadere che il limite:
- esista finito, allora l’integrale è convergente e la funzione è integrabile in senso improprio. L’integrale rappresenta un’area finita;
- esista infinito, allora l’integrale è divergente e la funzione non è integrabile in senso improprio. L’integrale rappresenta un’area infinita;
- non esista, allora l’integrale è indeterminato e la funzione non è integrabile in senso improprio. Non possiamo calcolare l’area.
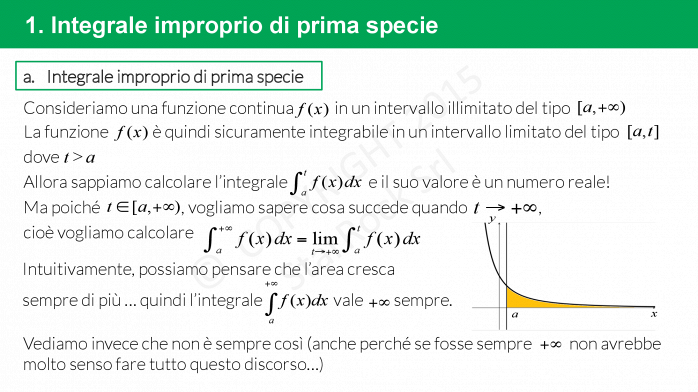
Integrale improprio di prima specie
Integrali impropri di prima, seconda e terza specie - Galleria
Gli integrali impropri sono di prima specie quando uno o entrambi gli estremi di integrazione sono infiniti.
La formula per risolvere un integrale improprio di prima specie è:
- £$\int_a^{+ \infty} f(x) \ dx = \lim\limits_{t \to \ + \infty} \int_a^t f(x) dx$£;
- £$\int_{- \infty}^a f(x) \ dx = \lim\limits_{t \to \ – \infty} \int_t^a f(x) dx$£;
- £$\int_{- \infty}^{+\infty} f(x) \ dx = \lim\limits_{t \to \ – \infty} \int_t^a f(x) dx +\lim\limits_{s\to + \infty}\int_a^s f(x) dx$£, con £$ a \in (- \infty, +\infty)$£.
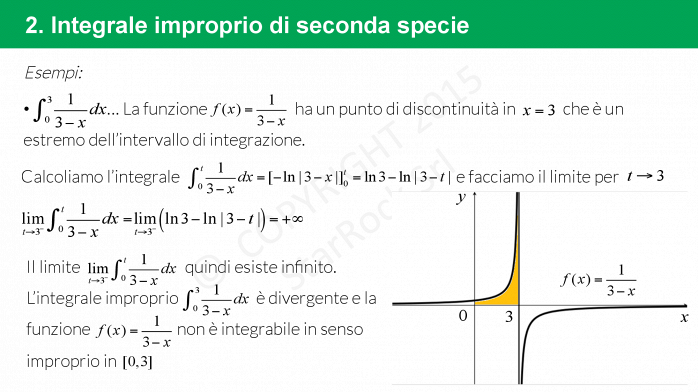
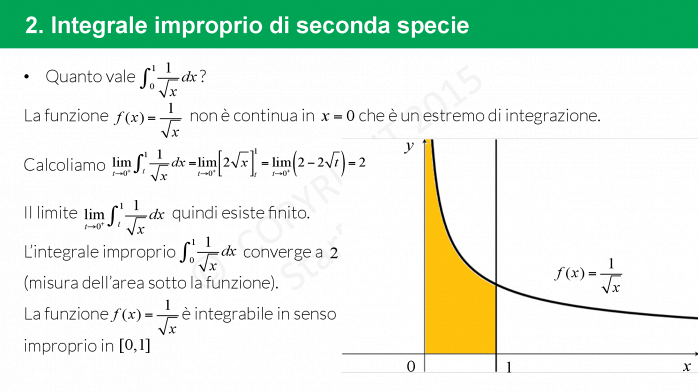
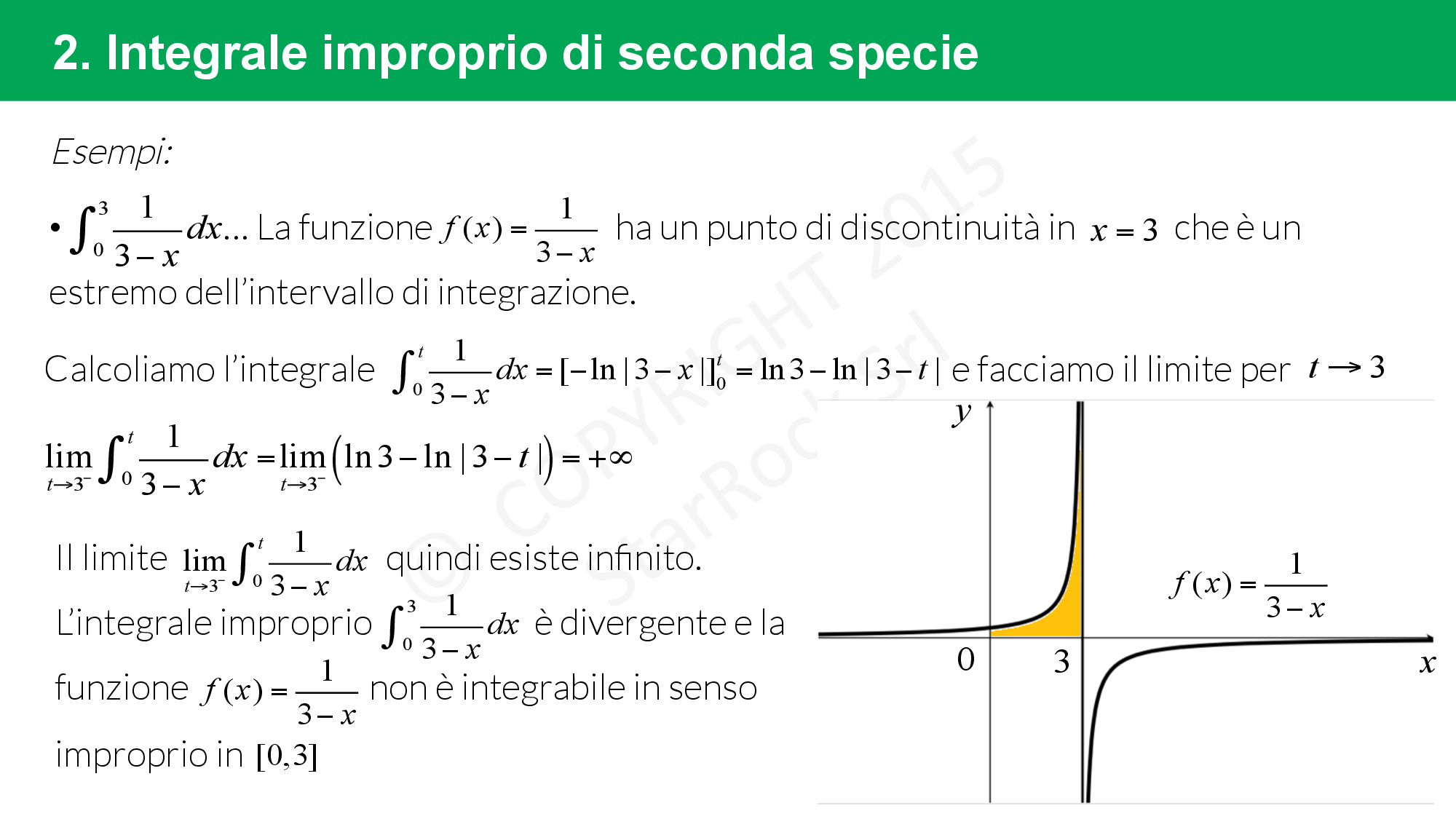
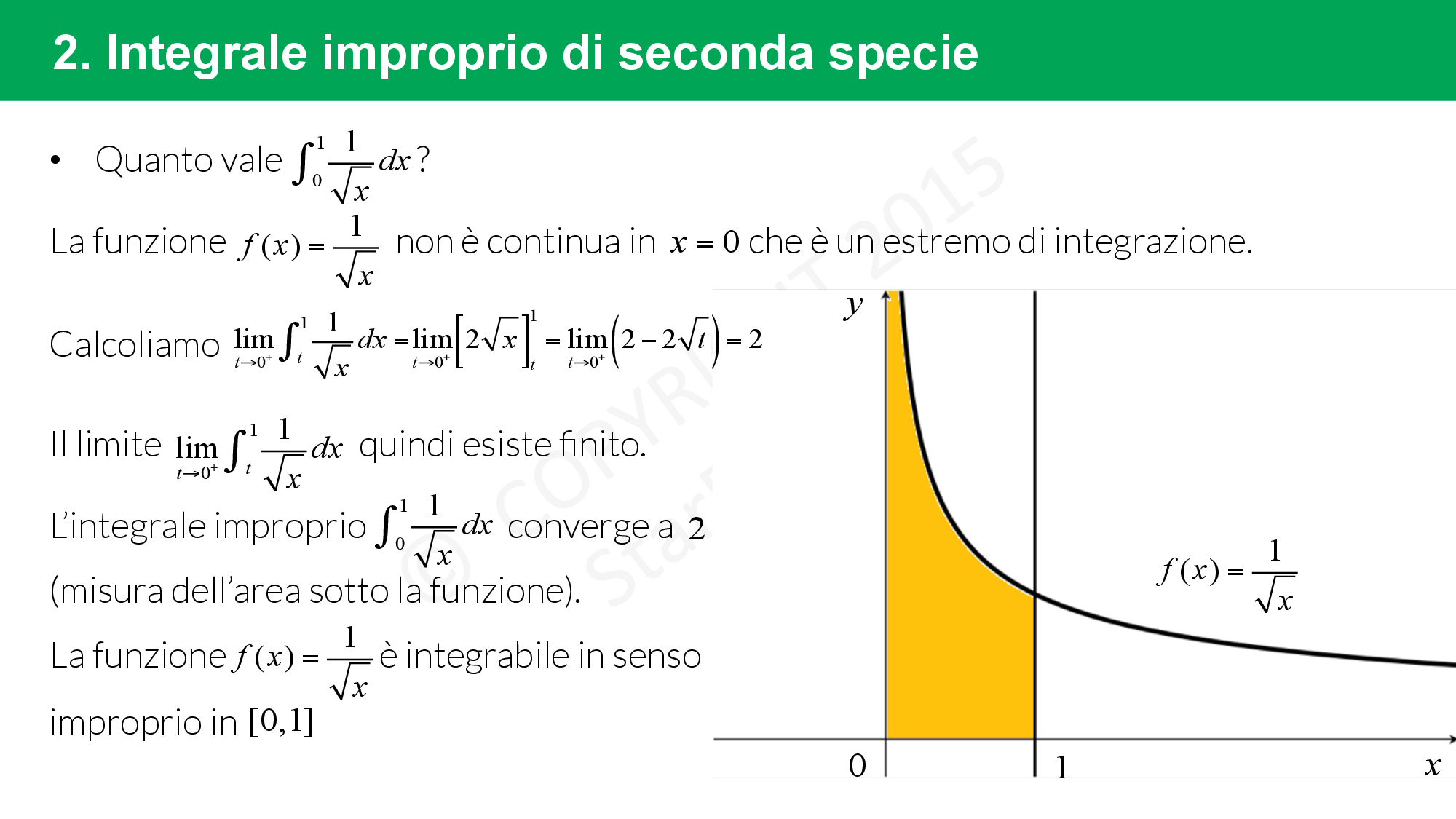
Integrale improprio di seconda specie
Integrali impropri di prima, seconda e terza specie - Galleria
Gli integrali impropri sono di seconda specie quando uno degli estremi di integrazione è un punto di discontinuità della funzione.
La formula per risolvere un integrale improprio di prima specie è:
- se £$ f(x)$£ ha dominio £$[a,b)$£, allora £$\int_a^{b} f(x) \ dx = \lim\limits_{t \to \ b} \int_a^t f(x) dx$£;
- se £$ f(x)$£ ha dominio £$(a,b] $£ allora £$\int_{a}^b f(x) \ dx = \lim\limits_{t \to \ a} \int_t^b f(x) dx$£.
Integrale improprio di terza specie
Integrali impropri di prima, seconda e terza specie - Galleria
Gli integrali impropri sono di terza specie quando nell’intervallo di integrazione c’è un punto di discontinuità per la funzione.
Sia £$c \in [a,b]$£ il punto di discontinuità per £$f(x)$£, allora puoi calcolare l’integrale di terza specie con la formula:
£$\int_{a}^{b} f(x) \ dx = \lim\limits_{t \to \ c^-} \int_a^t f(x) dx +\lim\limits_{t \to c^+}\int_t^b f(x) dx$£.
Esercizi sugli integrali impropri
Integrali impropri di prima, seconda e terza specie - Galleria
Allenati con gli esercizi sugli integrali impropri per arrivare preparato alla verifica o all’interrogazione!
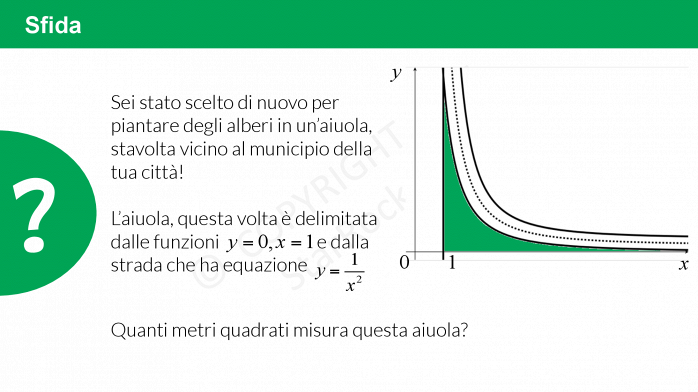
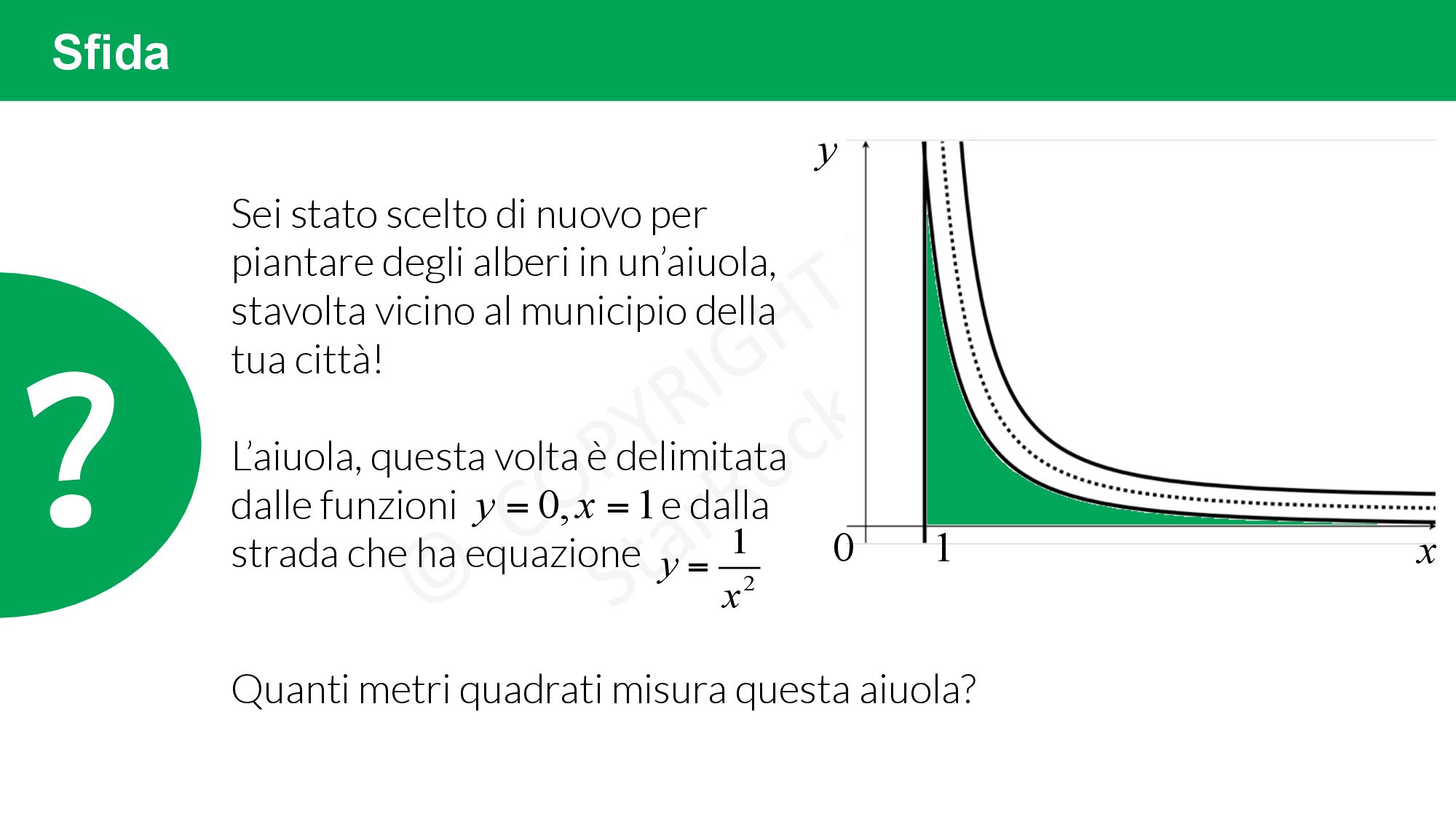
Sfida sugli integrali impropri
Testo e soluzione:
Integrali impropri di prima, seconda e terza specie - Galleria
Ancora a piantare alberi! Sì, ma questa volta l’aiuola ha una forma un po’ strana, sembra avere un’area infinita… Ma sarà realmente così?
Prova a risolvere la sfida sugli integrali impropri!