Gli angoli alla circonferenza e al centro: qual è la differenza

Riuscire a navigare nel mare intricato della geometria può sembrare una sfida titanica perché è piena di concetti e termini che possono sembrare incomprensibili finché non ci si prende un po’ la mano.

Tra questi, due concetti molto importanti sono l’angolo al centro e l’angolo alla circonferenza. Ma che cosa sono esattamente? E qual è la differenza tra i due? Non preoccuparti, lo capirai benissimo dopo aver letto il nostro articolo e aver ascoltato le nostre video-lezioni! A prima vista, un angolo sembra essere un angolo, ma come vedrete, la posizione e l’interazione di questi angoli con il cerchio determinano elementi differenti ai quali occorre prestare attenzione.

Gli angoli al centro, come suggerisce il nome, sono formati da due raggi che si estendono dal centro del cerchio a due punti sulla sua circonferenza. Gli angoli alla circonferenza, invece, sono formati da due segmenti di retta che toccano la circonferenza ma che si intersecano al di fuori del cerchio. Pronti? Cominciamo!

• Cos'è un angolo al centro
• Cosa sono gli angoli alla circonferenza
• Angolo al centro e angolo alla circonferenza: qual è la differenza
• La relazione tra gli angoli al centro e quelli alla circonferenza
• Le caratteristiche degli angoli al centro e angoli alla circonferenza
• Le proprietà degli angoli al centro
• Corollari sugli angoli alla circonferenza

Cos’è un angolo al centro

Ogni angolo che ha per vertice il centro della circonferenza si chiama angolo al centro.

Si dice che un angolo al centro £$ \alpha $£ insiste su un arco £$ \overgroup{AB} $£ dove £$ A $£ e £$ B $£ sono i due punti in cui i raggi intersecano la circonferenza. Su ogni arco £$ \overgroup{AB} $£ insiste un unico angolo al centro.

Cosa sono gli angoli alla circonferenza

Si dice angolo alla circonferenza ogni angolo che ha il vertice sulla circonferenza. I lati di un angolo alla circonferenza sono due semirette entrambe secanti la circonferenza o una tangente e una secante.

Su uno stesso arco £$ \overgroup{AB} $£ insistono infiniti angoli alla circonferenza, tutti della stessa ampiezza, ma un unico angolo al centro.

Angolo al centro e angolo alla circonferenza: qual è la differenza

Iniziamo con l’angolo al centro. Questo è formato da due raggi che partono dal centro di una circonferenza e raggiungono il suo perimetro. L’ampiezza di tale angolo dipende dalla distanza tra questi due raggi sulla circonferenza stessa: maggiore è la distanza, maggiore sarà l’angolo al centro.

D’altro canto, l’angolo alla circonferenza è un angolo il cui vertice si trova su una circonferenza, mentre i suoi lati sono secanti (linee che tagliano la circonferenza in due punti) o tangenti (linee che toccano la circonferenza in un solo punto). Contrariamente all’angolo al centro, la sua ampiezza non dipende direttamente dalla distanza tra le due secanti o tangenti, ma dalla posizione del suo vertice sulla circonferenza.

Ecco dove le cose diventano interessanti: c’è una relazione molto specifica tra l’angolo al centro e l’angolo alla circonferenza. Quando entrambi gli angoli sottendono la stessa corda della circonferenza, l’angolo al centro è sempre il doppio dell’angolo alla circonferenza. Questa proprietà, nota come “teorema degli angoli alla circonferenza“, è un pilastro fondamentale della geometria e può essere sfruttata in molti problemi geometrici complessi.

In conclusione, capire la differenza tra l’angolo al centro e l’angolo alla circonferenza è un passo essenziale nel padroneggiare la geometria. Con un po’ di pratica, questi concetti non sembreranno più così preoccupanti e vedrai che riuscirai a gestirli con molta più facilità!

La relazione tra gli angoli al centro e quelli alla circonferenza

Gli angoli al centro e gli angoli alla circonferenza sono legati tra loro.

Un angolo alla circonferenza e un angolo al centro che insistono su uno stesso arco si dicono corrispondenti. Ogni angolo al centro ha ampiezza doppia rispetto all’angolo alla circonferenza corrispondente.

Esempio: se l’angolo al centro misura £$ 2\alpha $£, il corrispondente angolo alla circonferenza avrà ampiezza £$ \alpha $£.

Tutti gli angoli alla circonferenza che insistono su uno stesso arco sono congruenti perché hanno tutti ampiezza uguale alla metà dell’angolo al centro corrispondente. Tutti gli angoli alla circonferenza che insistono su uno stesso arco £$ \overgroup{AB} $£ sono congruenti. Anche l’angolo limite, cioè l’angolo che ha il vertice in uno dei punti £$ A $£ o £$ B $£ e un lato tangente alla circonferenza, insiste sullo stesso arco £$ \overgroup{AB} $£, quindi è congruente a tutti gli altri.

Le caratteristiche degli angoli al centro e angoli alla circonferenza

Adesso parliamo degli angoli nelle circonferenze e delle loro proprietà.

Un angolo alla circonferenza è un angolo convesso che ha

• come vertice un punto sulla circonferenza;
• come lati due rette secanti la circonferenza, o una secante ed una tangente.

I lati di questo angolo delimitano un arco di circonferenza, quindi l’angolo insiste sull’arco.

Un angolo al centro è un angolo che ha

• come vertice il centro della circonferenza e;
• come lati due dei suoi raggi, che delimitano un arco di circonferenza.

L’angolo alla circonferenza è corrispondente ad un angolo al centro quando insiste sullo stesso arco.

Le proprietà degli angoli al centro

Teorema: Un angolo alla circonferenza è la metà del corrispondente angolo al centro.
Il primo caso è quello in cui un lato dell’angolo alla circonferenza coincide con un diametro. Possiamo utilizzare le proprietà del raggio e costruire un triangolo isoscele, applichiamo poi il teorema del triangolo isoscele sugli angoli alla base e quello degli angoli esterni di un triangolo, concludendo subito la dimostrazione.

Teorema: Un angolo alla circonferenza è la metà del corrispondente angolo al centro.
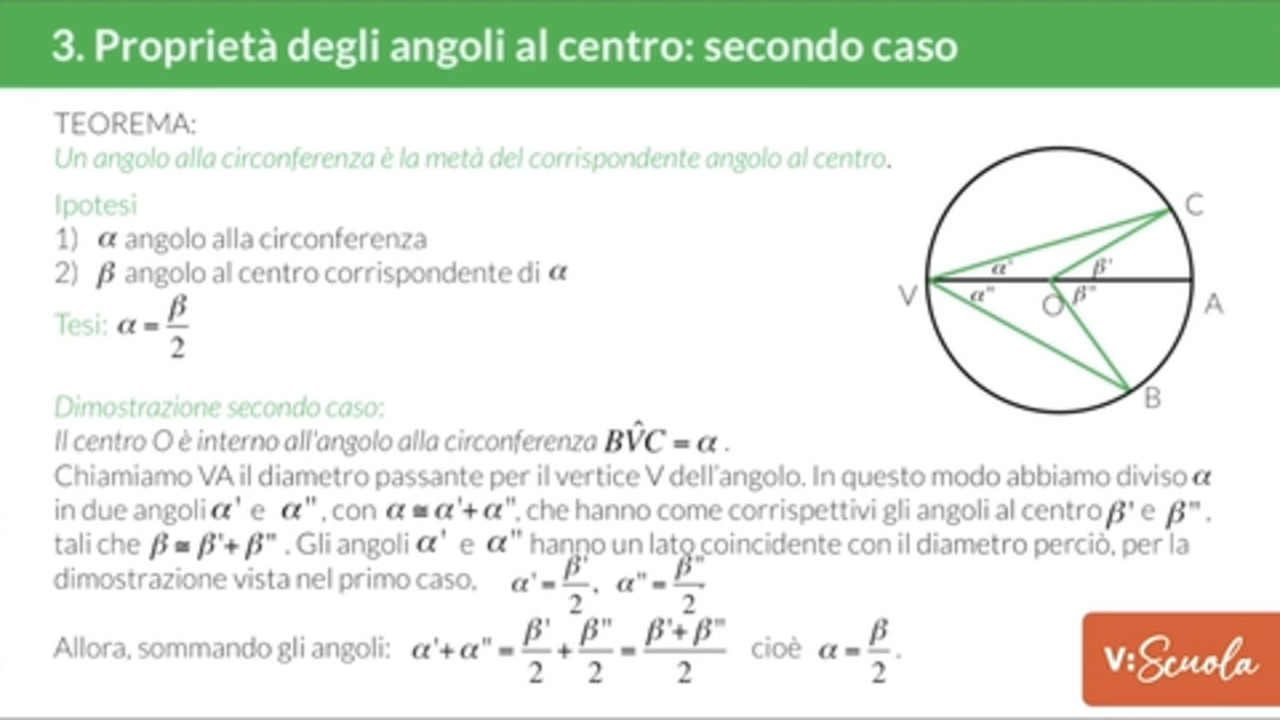
Il secondo caso è quello in cui il centro della circonferenza è interno all’angolo alla circonferenza.
Per dimostrarlo consideriamo il diametro passante per il vertice dell’angolo alla circonferenza che sarà così diviso in due angoli (la cui somma danno l’angolo iniziale), troviamo i due rispettivi angoli al centro e si usa la dimostrazione del caso 1 per concludere.

Teorema: Un angolo alla circonferenza è la metà del corrispondente angolo al centro.
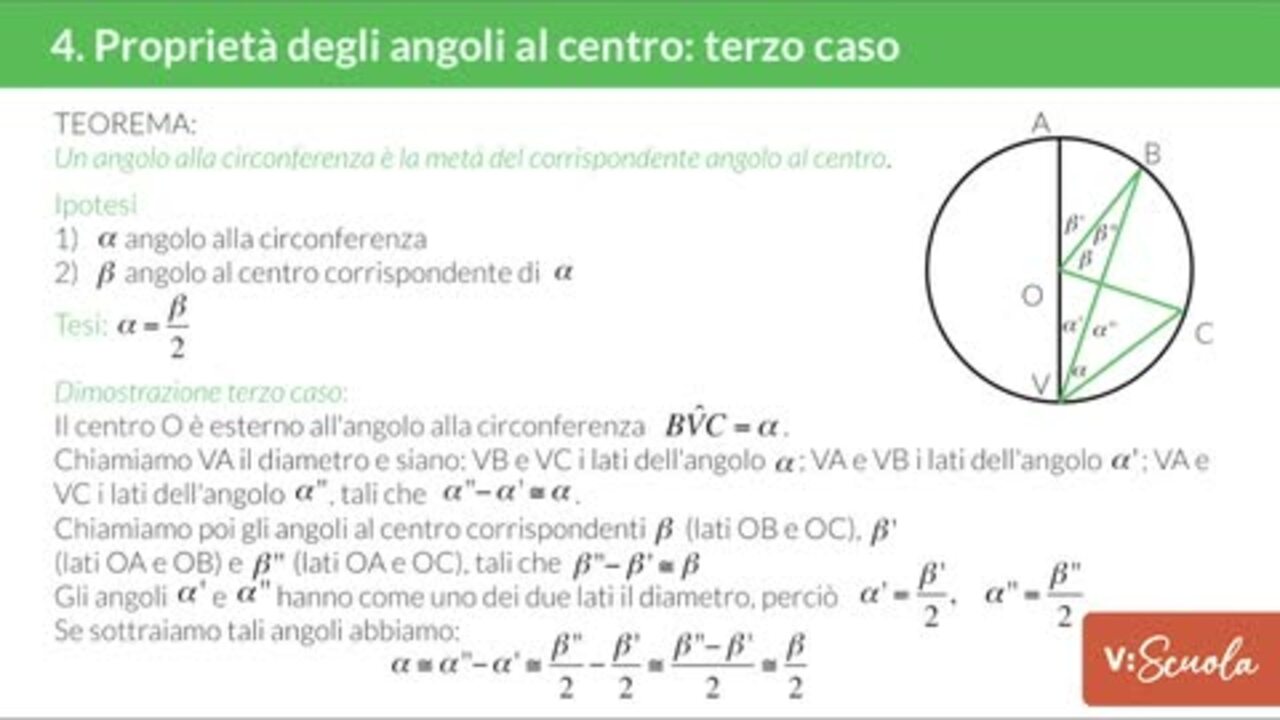
Il terzo caso è quello in cui il centro è esterno all’angolo alla circonferenza considerato.
Per la dimostrazione consideriamo il diametro passante per il vertice dell’angolo alla circonferenza considerato, troviamo così due angoli (la cui differenza dà l’angolo iniziale), troviamo i due rispettivi angoli al centro e concludiamo sfruttando i casi precedenti.

Corollari sugli angoli alla circonferenza

Corollario 1: Due o più angoli alla circonferenza che insistono sullo stesso arco sono congruenti.
Infatti, sono pari alla metà dello stesso angolo al centro e metà di angoli congruenti sono congruenti.

Corollario 2: Se un angolo alla circonferenza insiste su una semicirconferenza è retto.
Infatti è metà dell’angolo al centro che è un angolo piatto di £$180°$£.

Le possibili domande dell’interrogazione sugli angoli al centro e alla circonferenza

Cosa ti chiederà il prof all’interrogazione sugli angoli al centro e alla circonferenza?

Magari saranno proprio le domande che trovi in questo video! Se qualcosa non ti è chiaro riguarda le lezioni e poi allenati con gli esercizi!

Esercizi sugli angoli al centro e alla circonferenza

Sfida

Soluzione

Come si può tagliare una torta? Prova a risolvere la sfida sugli angoli al centro e gli angoli alla circonferenza.